Pool ball hits table, find an angle

  • Thread starter Thread starter mbrmbrg
  • Start date Start date
  • Tags Tags
    Angle Ball Table
AI Thread Summary
The discussion revolves around the physics of a cue ball's collision with a pool table rail, specifically analyzing the angles and momentum involved. The initial conditions include a cue ball with a mass of 0.165 kg and an initial speed of 1.60 m/s at an angle of 30.0°. The key questions are determining the angle theta_2 after the bounce and calculating the change in linear momentum. The participant initially struggles with the trigonometric relationships and the coordinate system used in the problem but ultimately arrives at the correct answer for theta_2, which is 30 degrees. The confusion stems from understanding the notation and angle measurement conventions in the context of the problem.
mbrmbrg
Messages
485
Reaction score
2
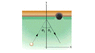
Figure 9-47 (attatched) shows a 0.165 kg cue ball as it bounces from the rail of a pool table. The ball's initial speed is 1.60 m/s, and the angle 1 = 30.0°. The bounce reverses the y component of the ball's velocity but does not alter the x component.

(a) What is theta_2?
(b) What is the change in the ball's linear momentum in unit-vector notation?

I got the physics of part b, the trig of part a is messing me up. I went so far as to make a system:
v\cos\theta_2=-v\cos\theta_1
v\sin\theta_2=v\sin\theta_1

As I thought! The angle must be in the second quadrant... so that means add 90 degrees, right? (And not 180-angle?)
But I don't know how to go from the typical coordinate system used for measuring angles to the funky one shown in the diagram.
 

Attachments

  • hrw7_9-47.gif
    hrw7_9-47.gif
    9.1 KB · Views: 709
Last edited:
Physics news on Phys.org
Never mind. I got the correct answer of 30 degrees (I had started out by saying theta_2 = -30 degrees). But why? How is that allowed? What kind of crazy notation are they using here (that apparently is standard...)?
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Momentum of ball on a pool table
Replies
12
Views
3K
Calculating Linear Momentum Change of a Bouncing Cue Ball | Physics Problem"
Replies
2
Views
20K
What is the final velocity and angle of ball 2 after collision on a pool table?
Replies
1
Views
3K
Impulse and Momentum: Ball and cart connected by a cord
Replies
24
Views
3K
Finding Angle of Sphere Falling From Table Edge
3
Replies
139
Views
11K
Balls elastic collision off center
Replies
7
Views
3K
Solving Pool Table Problem: Cue Ball Momentum Change
Replies
1
Views
7K
Ball Doing a Loop Min Kin Energy: Find Angle θ
Replies
7
Views
2K
How Do You Calculate the Final Speeds of Pool Balls After Collision?
Replies
5
Views
6K
How Can I Find the Initial Velocity of a Ball Based on Angle and Window Height?
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top