member 731016
- Homework Statement
- I am trying to derive the equation for a particle in uniform anti-clockwise circular motion. According to the lecture notes, this equation is ##\vec r(t) = (-Rsin(\omega t), Rcos(\omega t))##
- Relevant Equations
- ##\omega = \frac{d\theta}{dt}##
##\vec r(t) = (-Rsin(\omega t), Rcos(\omega t))##
To derive ##\vec r (t)=(−Rsin(ωt),Rcos(ωt)) ##
I start by integrating ##ω=\frac{dθ}{dt}## to get ##θ_f=θ_i+ωt##.
Therefore since ##Δθ=θ## by definition since the angular displacement is always taken with respect to some initial reference line, then ##θ_f−θ_i=θ## , thus, ##\theta = \omega t##.
Therefore, from ##x = r\cos\theta## we get ##x = r\cos\omega t## and for ##y = r\sin\theta = r\sin\omega t## which gives our position vector to be ##\vec r(t) = (r\cos\omega t, r\sin\omega t)##.
However, this is incorrect when compared to the lecture notes. Does someone please know what I did wrong here?
Here is a picture of the physical setup.
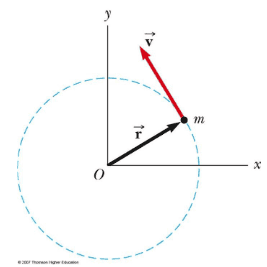
Many thanks!
I start by integrating ##ω=\frac{dθ}{dt}## to get ##θ_f=θ_i+ωt##.
Therefore since ##Δθ=θ## by definition since the angular displacement is always taken with respect to some initial reference line, then ##θ_f−θ_i=θ## , thus, ##\theta = \omega t##.
Therefore, from ##x = r\cos\theta## we get ##x = r\cos\omega t## and for ##y = r\sin\theta = r\sin\omega t## which gives our position vector to be ##\vec r(t) = (r\cos\omega t, r\sin\omega t)##.
However, this is incorrect when compared to the lecture notes. Does someone please know what I did wrong here?
Here is a picture of the physical setup.
Many thanks!