Potential and Electric Field near a Charged CD Disk

[cherry]

Homework Statement

A CD disk of radius ( R = 1 cm) is sprayed with a charged paint so that the charge varies continually with radial distance r from the center in the following manner: σ = - (3.5 C/m)r / R.
a) Find the potential at a point z = 5 cm above the center.
b) Find the strength of the electric field at this location.

Relevant Equations

V = kq/r

Hi! I am a very lost physics student here.

I got a) but I have no idea how.
The formula I used was from an online source and it was:

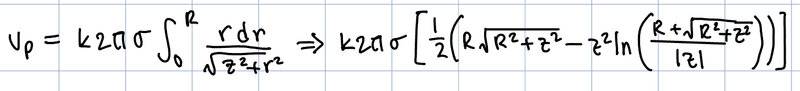
I think I need a contextual explanation of this formula before I attempt b).

My understanding of electric potential is that it is NOT potential energy, but rather energy per unit charge. I also know that the general formula for V is V = (kq) / r. Based on the question, it seems like the disk does not have a uniform charge distribution ("varies continually"). I also know that the distance between the charge and the disk (not the center) is expressed by sqrt( R^2 + z^2). That's about how far I understand this question.

Help would be much appreciated!

 

[haruspex]

sqrt( R^2 + z^2)

That's the distance from the given point to a point at the edge of the disc. For a point at radius r on the disc… well I'm sure you can figure that out.
The first step in the formula you found is elementary integration. You consider a small annulus of the disc between radii r and r+dr. Write down the charge on that annulus and divide it by the distance to the point to find the potential due to that annulus. Then integrate, i.e. add those up for all such annuli.

If you do not understand that then you need to take a refresher on integration.

 

[Delta2]

The general understanding is that the electrostatic potential is a volume, that is triple, integral of the charge density $\rho(\vec{x})$, and the general formula is obtained by solving Poisson's equation for electrostatics and it is given by
$$V(\vec{x})=\int\frac{\rho (\vec{x'})}{|\vec{x}-\vec{x'}|}d^3\vec{x'}$$
https://en.wikipedia.org/wiki/Poisson's_equation

Now of course I understand that this bizarre formula might baffle you. It can be simplified to a double or single integral depending if the charge density $\rho(x)$ is a function of three or two or one variables, each variable corresponding to a spatial dimension. Also you might ask what are $\vec{x}$ and $\vec{x'}$. Those are the position vectors in the field and source space respectively.

In your case this integral is simplified to a double integral. It is (in this case always, not in the general 3D case) $|\vec{x}|=z$ and $|\vec{x'}|=r$ where r the distance from the center of the disk. You will also need that also in our case (not in the general 3D case) it is $d^3\vec{x'}=rdrd\phi$ that is the surface element in polar coordinates. Also that for two vectors $a,b$ it is $$|\vec{a}-\vec{b}|=\sqrt{|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}|\cos(\vec{a},\vec{b})}$$ where $(\vec{a},\vec{b})$ is the angle between vectors a, b.

I know that this whole post of mine might baffle you right in the middle of your brain. If that's the case just ignore it and follow @haruspex post.