Linus Pauling
- 187
- 0
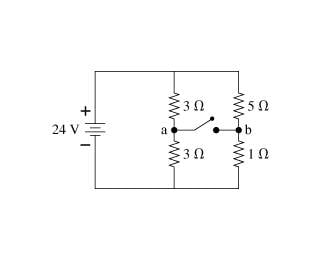
1. What is the potential difference DeltaVab between points a and b when the switch is open? Closed?
2. DeltaV = IR
3. I solved I for the battery, which is 8A. What do I use for my R value to solve for DeltaV between a and b, though? I tried, for example, DeltaV = IR = 8A*6ohms = 48V. I guess I'm confused as to what I use for R to calculate the potential at each point, which are the values I use to get my answer. Could someone explain this to me conceptually? For the potential at A, for example, I tried multiplying the current (8A) by 3ohms because the current flows through that 3ohm resistor to get to point A...
2. DeltaV = IR
3. I solved I for the battery, which is 8A. What do I use for my R value to solve for DeltaV between a and b, though? I tried, for example, DeltaV = IR = 8A*6ohms = 48V. I guess I'm confused as to what I use for R to calculate the potential at each point, which are the values I use to get my answer. Could someone explain this to me conceptually? For the potential at A, for example, I tried multiplying the current (8A) by 3ohms because the current flows through that 3ohm resistor to get to point A...