Potential due to a rod with a nonuniform charge density

[archaic]

Homework Statement

A rod of length $L$ lies on the x-axis such that its left tip is at the origin. It's charged and has a nonuniform charge density $\lambda=\alpha x$, where $\alpha>0$.
What is the potential at a point $B$ on its bisector? (Use the following as necessary: α, k, L, b, and d.)

Relevant Equations

$$dV=k\frac{dq}{r}$$

I'm not sure I understand why I need to use $d$.. Maybe they want me to have the potential be zero at $A$?

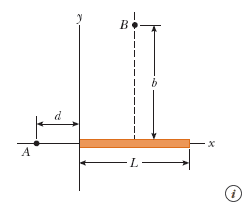
In any case, I have found$$V(B)=\alpha k\int_0^L\frac{x}{\sqrt{b^2+\left(x-\frac{L}{2}\right)^2}}dx+C=\frac{\alpha kL}{2}\ln\left(\frac{\sqrt{L^2+4b^2}+L}{\sqrt{L^2+4b^2}-L}\right)+C$$and$$V(A)=\alpha k\int_0^L\frac{x}{d+x}dx+C=\alpha k\left(L+d\ln\left(\frac{d}{L+d}\right)\right)+C$$

 

[haruspex]

I'm not sure I understand why I need to use $d$..
In any case, I have found$$V(B)=\alpha k\int_0^L\frac{x}{\sqrt{b^2+\left(x-\frac{L}{2}\right)^2}}dx+C=\frac{\alpha k}{2}\ln\left(\frac{\sqrt{L^2+4b^2}+L}{\sqrt{L^2+4b^2}-L}\right)+C$$

It says to use the variables as necessary. If it is not necessary don’t use it.

I get a different result for the integration. Yours seems to be dimensionally wrong.
I also tried checking yours by fixing the total charge at Q and letting L tend to zero. I got that it tends to infinity as $\frac {kQ}{Lb}$ instead of tending to $\frac {kQ}{b}$.

 

[archaic]

It says to use the variables as necessary. If it is not necessary don’t use it.

I get a different result for the integration. Yours seems to be dimensionally wrong.
I also tried checking yours by fixing the total charge at Q and letting L tend to zero. I got that it tends to infinity as $\frac {kQ}{Lb}$ instead tending to $\frac {kQ}{b}$.

I forgot a factor of $L$.. It's fixed now. Thank you!
You probably have found $\alpha kL\,\mathrm{arsinh}(\frac{L}{2b})$, they're similar.
That's not the desired result, though..