Potential inside a rectangular pipe

[better]

TL;DR Summary: Independence of potential( inside a rectangular pipe running along z axis)from z coordinate

Consider the following diagram

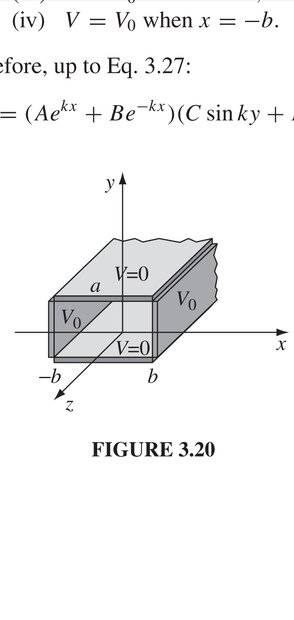
It is an infinite rectangular pipe running along z axis.I know that the potential inside the pipe is independent of z coordinate, but I cannot seem to convince myself of it.My guess is that it has to do something with uniqueness theorem.

 

[berkeman]

Welcome to PF. I've moved your thread to the schoolwork forums.

What equations would apply to this problem?

 

[haruspex]

My guess is that it has to do something with uniqueness theorem.

Symmetry, I'd have said. Everywhere along the axis looks like everywhere else.