Power Loss Due to An Eddy Current

[BlackMelon]

TL;DR

Finding power loss due to eddy current
Reference website: https://www.electricalvolt.com/2019/08/eddy-current-loss-formula/?expand_article=1

Hi there!

Recently, I am studying this kind of power loss from the following link:
https://www.electricalvolt.com/2019/08/eddy-current-loss-formula/?expand_article=1
Just to summarize an idea,

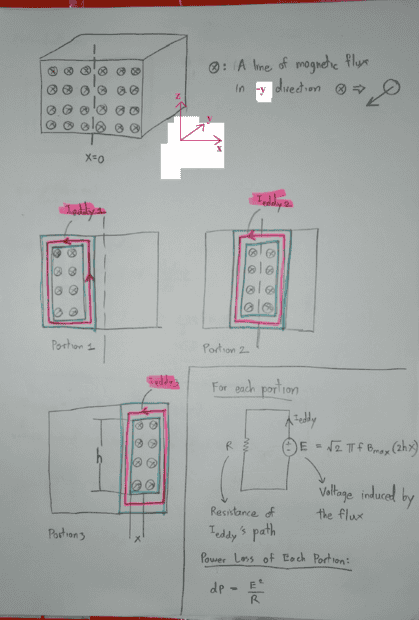
Supposed that we got a material, which is penetrated by a magnetic flux. The material will generate the eddy current to oppose the change of the flux.
We divide this material into portions.
We treat each of the portion as a one-turn coil, having I_eddy flowing through.
Use the Faraday's Law to find the induced voltage (E) in each portion.
Use R = rho*(length)/(area) to find the resistance of each portion (that I_eddy flows through)
The power loss of each portion is dP = E^2/R
Integrate dP over all the portions to get "P: The power loss due to eddy current."

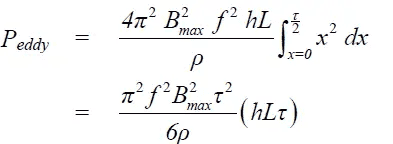
From this equation in the link, I am curious why the bounds of the integration is 0 to T/2. Should it be -T/2 to +T/2 instead?
(Please look at the diagram in the aformentioned link)

Best Regards,
BlackMelon

 

[DaveE]

Your diagram is hard to read as posted, although not impossible. I don't see any "T", or, "τ", which is what I think you meant. Don't make it hard for people to help you, they may just give up and move on. Please communicate clearly, we are not clairvoyant.

 

[BlackMelon]

Hi All,
I'm sorry for the my unclear drawing. Please download it from here:
https://www.mediafire.com/file/tftzo99pddsvzhj/EddyCurrentLoss.png/file

According to the diagram in this link:
https://www.electricalvolt.com/2019/08/eddy-current-loss-formula/?expand_article=1
T and τ are the same. It is said "Let the length, height and thickness of the laminated sheet is L,h and𝞃 respectively". However on the diagram, the thickness is represented by T, instead of 𝞃. The dotted line represents the reference position, where x = 0.

 

[Gavran]

The interval of the integration is $[0, \frac \tau 2]$ because the interval $[-\frac \tau 2, 0]$ is already included into the integration through the formula for the area which is $A = 2 h x = 2 \cdot h x$ and through the formula for the resistance which is $R = \rho \cdot \frac {2 h + 4 x} {L dx} = 2 \cdot \rho \cdot \frac {h + 2 x} {L dx}$.

If the interval of the integration is $[-\frac \tau 2, \frac \tau 2]$ the formula for the area will be $A = h x$ , the formula for the resistance will be $R = \rho \cdot \frac {h + 2 x} {L dx}$

and there will be next:

$\Phi (t) = B (t) \cdot A = B_{max} \cdot \sin (\omega t) \cdot h x$

$E = \frac {\sqrt 2} {2} \cdot B_{max} \cdot 2 \pi f \cdot h x$
$E = \sqrt 2 \cdot B_{max} \cdot \pi f \cdot h x$

$dP = \frac {E^2} {R}$
$dP = E^2 \cdot \frac {L dx} {\rho \cdot (h + 2 x)}$
$dP = E^2 \cdot \frac {L dx} {\rho \cdot h}$
$dP = (\sqrt 2 \cdot B_{max} \cdot \pi f \cdot h x)^2 \cdot \frac {L dx} {\rho \cdot h}$
$dP = 2 \cdot B_{max}^2 \cdot \pi^2 f^2 \cdot h^2 x^2 \cdot \frac {L dx} {\rho \cdot h}$
$dP = 2 \cdot B_{max}^2 \cdot \pi^2 f^2 \cdot h x^2 \cdot \frac {L dx} {\rho}$

$P_{eddy} = \frac {2 \pi^2 \cdot B_{max}^2 \cdot f^2 \cdot h L} {\rho} \cdot \int_{-\frac \tau 2}^{\frac \tau 2} x^2 \, dx$
$P_{eddy} = \frac{2 \pi^2 \cdot B_{max}^2 \cdot f^2 \cdot h L} {\rho} \cdot (\int_{-\frac \tau 2}^{0} x^2 \, dx + \int_{0}^{\frac \tau 2} x^2 \, dx)$
$\int_{-\frac \tau 2}^{0} x^2 \, dx = \int_{0}^{\frac \tau 2} x^2 \, dx$
$P_{eddy} = \frac{2 \pi^2 \cdot B_{max}^2 \cdot f^2 \cdot h L} {\rho} \cdot (\int_{0}^{\frac \tau 2} x^2 \, dx + \int_{0}^{\frac \tau 2} x^2 \, dx)$
$P_{eddy} = \frac{2 \pi^2 \cdot B_{max}^2 \cdot f^2 \cdot h L} {\rho} \cdot 2 \int_{0}^{\frac \tau 2} x^2 \, dx$
$P_{eddy} = \frac {4 \pi^2 \cdot B_{max}^2 \cdot f^2 \cdot h L} {\rho} \cdot \int_{0}^{\frac \tau 2} x^2 \, dx$
$P_{eddy} = \frac{\pi^2 \cdot f^2 \cdot B_{max}^2 \tau^2 } {6 \rho}\cdot (h L \tau)$
.