LagCompensator
- 24
- 1
< Mentor Note -- thread moved to HH from the technical forums, so no HH Template is shown >[/color]
Hi,
I have the following circuit, where V2 is found to be 0.964∠-3.3 (degrees) p.u.
Then I am to find the reactive power supplied by the capacitor bank (j0.25 p.u, to the right). I got the right number, but with wrong sign, could anyone parhaps tell me if my proposal at the end here is correct?
Calculations:
Current down the capacitor branch:
I_{c} = V_{2} \times Y_{c} = (0.964 \angle-3.3) \times j0.25 = 0.241 \angle 86.7 p.u.\\<br /> S = V \times I^{*} \rightarrow S_{c} = V_{2} \times I_{c}^{*} = 0.964 \angle(-3.3) \times 0.241 \angle(-86.7) = -j0.2323 p.u.<br />
So I get that Q = -0.2323, however it should have been positive since the bank is supplying the bus with power, and since injected power into a bus is defined positive.
So then I guess that current is defined as positive when entering the bus, and negative when leaving, and because of that I_c should be calculated like this instead:
I_{c} = (0 - V_{2}) \times Y_{c}
Thanks for any feedback.
Best regards
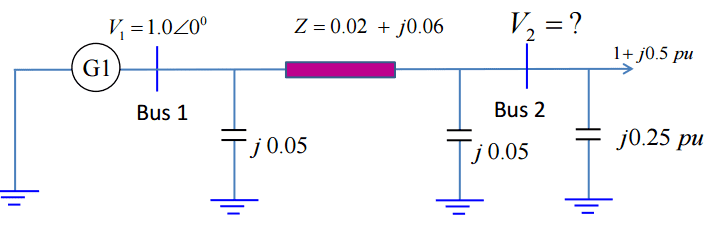
Hi,
I have the following circuit, where V2 is found to be 0.964∠-3.3 (degrees) p.u.
Then I am to find the reactive power supplied by the capacitor bank (j0.25 p.u, to the right). I got the right number, but with wrong sign, could anyone parhaps tell me if my proposal at the end here is correct?
Calculations:
Current down the capacitor branch:
I_{c} = V_{2} \times Y_{c} = (0.964 \angle-3.3) \times j0.25 = 0.241 \angle 86.7 p.u.\\<br /> S = V \times I^{*} \rightarrow S_{c} = V_{2} \times I_{c}^{*} = 0.964 \angle(-3.3) \times 0.241 \angle(-86.7) = -j0.2323 p.u.<br />
So I get that Q = -0.2323, however it should have been positive since the bank is supplying the bus with power, and since injected power into a bus is defined positive.
So then I guess that current is defined as positive when entering the bus, and negative when leaving, and because of that I_c should be calculated like this instead:
I_{c} = (0 - V_{2}) \times Y_{c}
Thanks for any feedback.
Best regards
Last edited by a moderator: