Predicted sizes of (observable) universe

[nomadreid]

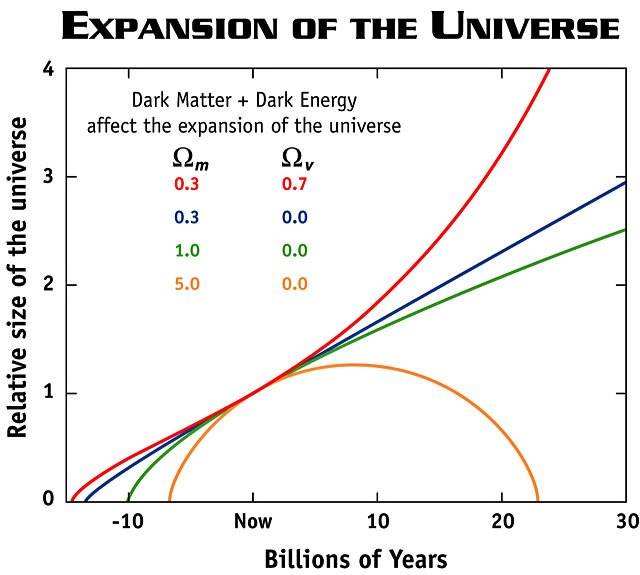
I have read the advice of Nugatory and Jorrie in order to get me started on understanding cosmology; I have played around with the cited calculators (except http://www.einsteins-theory-of-relativity-4engineers.com/CosmoLean_A20.html doesn't open for me), without mastering them, and read for a few hours. It may take me until the Heat Death of the universe to understand much of it, but I will start with a couple of very elementary questions. I refer to the simplified graph in the attachment. (a) We are talking about the red line, I presume, based on present knowledge? (b) Is "relative size" referring to comoving distance diameter, the proper distance diameter, or a volume? ("Size" is ambiguous.)

 

[Bandersnatch]

(a) We are talking about the red line, I presume, based on present knowledge?

Yes. The red line is the only one that gives you a period of deceleration followed by acceleration.

(b) Is "relative size" referring to comoving distance diameter, the proper distance diameter, or a volume? ("Size" is ambiguous.)

That is the scale factor $a(t)$. The factor by which all distances* differ from today's (it's scaled to 1 being 'like today').
Comoving distances by definition don't change with expansion.
Proper distance and comoving distance are related by $d(t)=a(t)x_0$ where the comoving distance $x_0$ is defined as the proper distance at the present epoch.

So, if the proper distance to the stuff that today is at the edge of the observable universe is 45 Gly, it is also the comoving distance to it. To get the proper distance to that same stuff at some time in the past when the scale factor was equal to 1/1000th, you just multiply 45 Gly by 1/1000th.

*large scale only

(btw, Jorrie's calculator doesn't open for me either today. Perhaps the website is temporarily down.)

 

[Jorrie]

(btw, Jorrie's calculator doesn't open for me either today. Perhaps the website is temporarily down.)

Sorry guys, due to a lost and blocked credit card, my hosting did not renew and I realized too late. :( Working on it...

 

[nomadreid]

Thanks, Bandersnatch! (and good luck, Jorrie.) So, if I may try a simple calculation from the graph, in 20 billion years, the comoving distance will add 20 Gly to the present 45 Gly, totalling 65 Gly comoving distance, but then taking the factor of 3 from the graph, the proper distance will be 45+3(20) =105 Gly?

Does a(t) follow a particular formula that could be used to extrapolate forward in time beyond the limits of this graph, or would that be too speculative?

 

[Jorrie]

Thanks, Bandersnatch! (and good luck, Jorrie.)

The site is up and running again ;) BTW, use the link in my signature below. The one that you quoted should still work, but it is quite ancient by the pace of developments today...

 

[Jorrie]

So, if I may try a simple calculation from the graph, in 20 billion years, the comoving distance will add 20 Gly to the present 45 Gly, totalling 65 Gly comoving distance, but then taking the factor of 3 from the graph, the proper distance will be 45+3(20) =105 Gly?

No, I don't think it works like that. You simply take the scale factor off the graph, a(t=now+20) ~ 3 and multiply the present proper distance by that. So it is 3 times 45 = 135 Gly.

But take note that this is just the future proper distance to a hypothetical emitter that happens to be 45 Gly from us at the moment. We have never and will never observe such an emitter, except if we are able to detect gravitational waves from there in the future. It is also not the radius of the observable universe, because it grows by a different 'law'.

I have summarized all the equations that Lightcone7 use in this Insights post: https://www.physicsforums.com/insights/lightcone7-tutorial-part-iii-things-computed/
Ask if not clear.

 

[Jorrie]

Does a(t) follow a particular formula that could be used to extrapolate forward in time beyond the limits of this graph, or would that be too speculative?

I had to search quite a way back, but George Jones has previously posted a generalized equation for the evolution of a(t), valid for a spatially flat universe with negligible radiation energy.
a\left(t\right) = A \sinh^{\frac{2}{3}} \left(Bt\right)
A = \left( \frac{1 - \Omega_{\Lambda 0}}{\Omega_{\Lambda 0}} \right)^{\frac{1}{3}}
B = \frac{3}{2} H_0 \sqrt{\Omega_{\Lambda 0}}
If t is in Gyr, then Ho must be in Gyr^-1 and \Omega_{\Lambda 0} is the present density parameter of the cosmological constant (0.69).

This gives a(t) = 3.37 at 20 Gyr into the future (t=33.8 Gyr).

 

[Chalnoth]

I had to search quite a way back, but George Jones has previously posted a generalized equation for the evolution of a(t), valid for a spatially flat universe with negligible radiation energy.
a\left(t\right) = A \sinh^{\frac{2}{3}} \left(Bt\right)
A = \left( \frac{1 - \Omega_{\Lambda 0}}{\Omega_{\Lambda 0}} \right)^{\frac{1}{3}}
B = \frac{3}{2} H_0 \sqrt{\Omega_{\Lambda 0}}
If t is in Gyr, then Ho must be in Gyr^-1 and \Omega_{\Lambda 0} is the present density parameter of the cosmological constant (0.69).

This gives a(t) = 3.37 at 20 Gyr into the future (t=33.8 Gyr).

Something seems wrong there. In the limit that $\Omega_\Lambda = 1$, $a(t) = 0$. It should be $a(t) = e^{H_0 t}$. The result also diverges for $\Omega_\Lambda = 0$.

 

[Jorrie]

Something seems wrong there. In the limit that $\Omega_\Lambda = 1$, $a(t) = 0$. It should be $a(t) = e^{H_0 t}$. The result also diverges for $\Omega_\Lambda = 0$.

George did have the caveat: "For a spatially flat universe that consists of matter and dark energy (w = -1), but no radiation, "...

I think the presence of matter invalidates $a(t) = e^{H_0 t}$.

 

[Chalnoth]

George did have the caveat: "For a spatially flat universe that consists of matter and dark energy (w = -1), but no radiation, "...

I think the presence of matter invalidates $a(t) = e^{H_0 t}$.

Sure, but it should at least approach that in the limit. I don't think it does. Therefore, I'm pretty sure this solution is approximate rather than exact. Or there's a typo somewhere.

 

[Jorrie]

Sure, but it should at least approach that in the limit. I don't think it does. Therefore, I'm pretty sure this solution is approximate rather than exact. Or there's a typo somewhere.

It is approximate due to the presence of radiation, so it cannot be used for the early universe. As radiation diminishes it becomes more and more accurate. Further, for a flat universe, $\Omega_\Lambda$ approaches but never reaches 1 in the distant future. So I think the accuracy is maintained forever, well almost...

 

[Chalnoth]

It is approximate due to the presence of radiation, so it cannot be used for the early universe. As radiation diminishes it becomes more and more accurate. Further, for a flat universe, $\Omega_\Lambda$ approaches but never reaches 1 in the distant future. So I think the accuracy is maintained forever, well almost...

My analysis of the extreme cases doesn't assume any radiation.

 

[Jorrie]

My analysis of the extreme cases doesn't assume any radiation.

OK, we can split hairs, or just put an approx sign instead of the equality; but George's conditions don't quite allow the extreme cases.

In any case, I hope it answers the OP's question adequately.

 

[nomadreid]

Thanks for all that, Jorrie and Chalnoth! It is taking me a while to work through all this (and annoying details like work get in the way of this more enjoyable activity), but your answers will be a tremendous help in getting me to understand the topic better. I am very grateful.