vcsharp2003
- 915
- 179
- Homework Statement
- A and B having equal skill, are playing a game of three points. After A has won 2 points and B has won 1 point, what is the probability that A will win the game?
Above is problem# 22.18 from Schaum's Outline of College Mathematics. It's an unsolved problem in the book with the answer given as ##\frac{3} {4}##
- Relevant Equations
- For an experiment that can have multiple outcomes, ##P(X) = \frac {n(X)} {n(S)}## where ##P(X)## is probability that event X will occur, ##n(X)## is number of ways in which event X can occur, ##n(S)## is total number of ways in which all possible events can occur
I tried to solve this problem using the chart given below. But I get a different answer of ##\frac {2}{3}## rather than ##\frac {3}{4}##. Maybe the answer given is incorrect?
I determine from the chart the number of ways in which A could win given that A has already won 2 of first 3 points; from the chart it clearly shows circled A's as these wins. The number of circled A's is 6.
Now I determine the total number of ways in which all possible events can occur given that A has already won 2 of first 3 points. From the chart, it is clearly 9.
$$\therefore P(X) = \frac {6} {9} =\frac{2} {3}$$
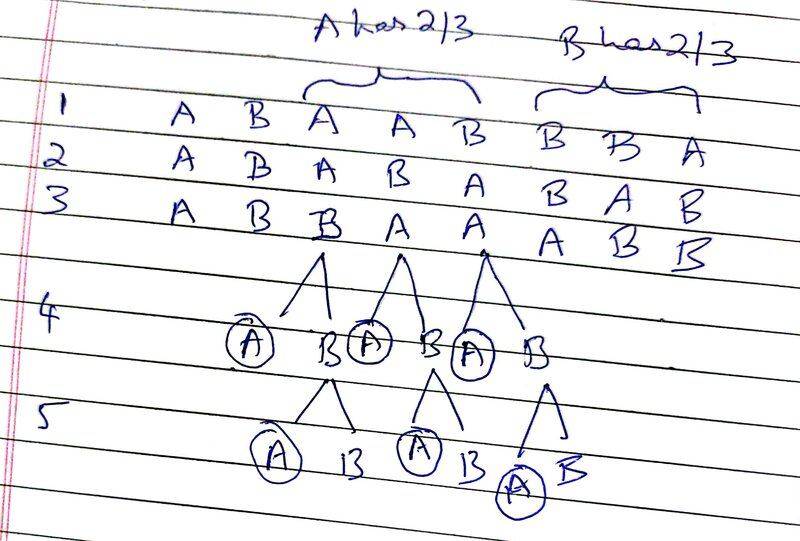
I determine from the chart the number of ways in which A could win given that A has already won 2 of first 3 points; from the chart it clearly shows circled A's as these wins. The number of circled A's is 6.
Now I determine the total number of ways in which all possible events can occur given that A has already won 2 of first 3 points. From the chart, it is clearly 9.
$$\therefore P(X) = \frac {6} {9} =\frac{2} {3}$$
Last edited: