- #1
Shell_E
- 3
- 1
Thank you advance for help!
So the problem is find <x> in P space.
The solution's logic is use formula:
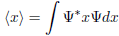 The submit with
The submit with
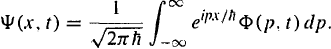 Then one will get the integral
Then one will get the integral
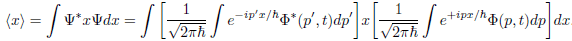
by noticing that
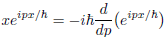 , one can replace xeipx/ħ in the integral
, one can replace xeipx/ħ in the integral
so that
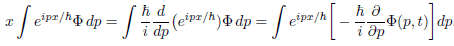
and then after solving the integral one can find the expectation value for x.
The part I don't understand is why
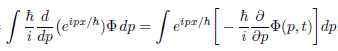 , firstly I am not sure where is the minus sign comes from. Next I don't think I can just change the order of eipx/ħ and Φ because the term d/dp.
, firstly I am not sure where is the minus sign comes from. Next I don't think I can just change the order of eipx/ħ and Φ because the term d/dp.
Could anyone help me figure the integral out?
Thank you everybody.
Shell
So the problem is find <x> in P space.
The solution's logic is use formula:
by noticing that
so that
and then after solving the integral one can find the expectation value for x.
The part I don't understand is why
Could anyone help me figure the integral out?
Thank you everybody.
Shell