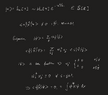martinbn
Science Advisor
- 4,347
- 2,408
Which book/source do you follow?gaiussheh said:Well, that is actually where my confusion starts. I take an operator to be a map from a function to a function. It may not be closure in the Hilbert space, so people usually restrict its domain to, for example, the Schartz space. I just do not understand the rationale behind this. As long as your function decays faster than ##\mathrm{e}^{-x^2}##, in integrate ##\displaystyle \int f[x] \mathrm{e}^{-x^2} g[x] \mathrm{d} x## converge and it is still self adjoint. So, similar to restricting wavefunctions to the Schwartz space, you can say that the operator ##\mathrm{e}^{-x^2}## has a smaller domain and is still self-adjoint. This never comes to an end, so why would one ever do this at the beginning?