diffidus
- 5
- 1
- Homework Statement
- I am trying to understand example 13.6 given in the book 'Quantum Field Theory for the Gifted Amateur' by Lancaster and Blundell. The problem is: Consider a massive photon in the rest frame so that P^μ=([m,0,0,0). If we boost the particle in the z direction to P^μ=([E,0,0,p) can we calculate the product of the polarisation vectors:
- Relevant Equations
- I have included the relevant equations below. I tried multiplying the matrices together but could not get the correct answer. Is there anybody out there that can help?
Before boost we have
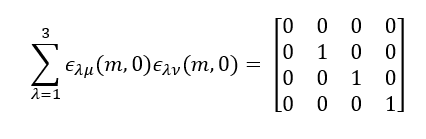
Then using the Lorentz boost:
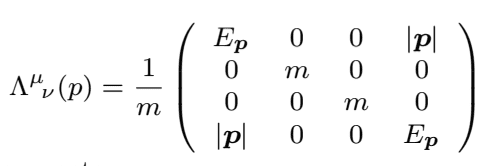
I want to calculate:
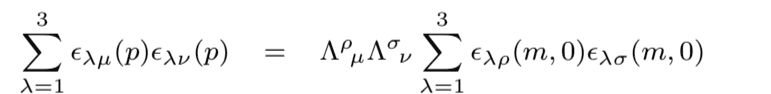
I tried multiplying the matrices together but I never get the stated answer which should be:
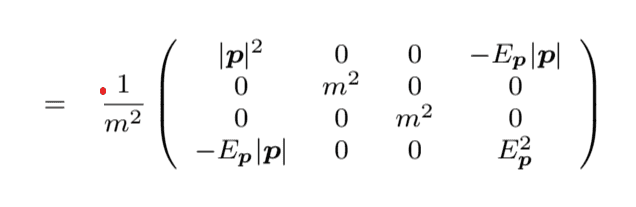
Then using the Lorentz boost:
I want to calculate:
I tried multiplying the matrices together but I never get the stated answer which should be: