- #1
Laura1321412
- 24
- 0
Homework Statement
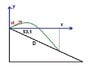
A skier leaves the ramp of a ski jump with a velocity of 10.7 m/s, 15.8° above the horizontal. The slope is inclined at 51.3°, and air resistance is negligible. Calculate the distance from the ramp to where the jumper lands.
Homework Equations
Kinematics ones
The Attempt at a Solution
I assumed an x-axis along the height of the ramp, and developed equations for the curve of the skier and the line of the slope of the hill..
first, distance to from slope to highest point of jump
vi(y) = sin15.8 *10.7 = 2.9134 /9.8 = t = .29728 , 2.9134 +0 /2 * t = .4331 m
So the y distance of the jumper should equal the distance he has fallen at time (t) +.4331
x = (t+.2972)*cos15.8 *10.7
y= -4.9t^2 +.4331
these are only valid for t> 2.9134 but that shouldn't matter?
sooo tan 51.3 *1 = 1.248 is the slope of the line the x and y distance need to intersect... sloping downard from the angle of the jump so it will be negative
okay , solving for t(x) -->10.296t + 3.06=x , (x-3.06)/10.296= t
plug this into the y distance equation
-4.9 [ (x-3.06)/10.296 ]^2 +.4331
-4.9 [( x^2 -6.12x +9.364)/ 106] +.4331
(-4.9x^2 + 29.99x - 45.88)/106 +.4331
-.0462x^2 + .283x -.00027 = y
now the line it needs to intersect, slope found above, since it originates from the jump which determined as the axis, the equation should by y= -1.238x
equate these equations
-.0462x^2 + .283x -.00027 = -1.238x
-.0462x^2 + 1.52x -.00027 = 0
x= 32.9 m
with this distance the time would be 3.2 s, making the y distance .5*9.8(3.2-.297)^2 = 41.3 -.433 (measured from jump height not from heighest point of projection ) 40.9 m ... the slope of these two distances i pretty close to the desired one (i have rounded messily and a bunch, will redo + fix ...)
so, the total distance down the jump would be sqrt ( x^2 +y ^2 )
= 52.5 m
Im unsure of this answer, i just wanted to know if anyone can see a mistake i made? I really am completley lost as to if i went about solving this correctly. Also, since the slope of the this line is negative, do i report it as a negative distance?
Thank you ! :)