Find v_1 for projectile using start position, final position and angle

[GreyNoise]

Homework Statement

A canon located 60.0 m from the base of a vertical 25.0 m cliff, shoots a 15 kg shell at 43 degrees above the horizontal toward the cliff. What must be the minimum muzzle velocity, v1, for the shell to clear the top of the cliff?

Relevant Equations

v_2y = v_1y - gt
(v_2y)^2 = (v_1y)^2 - 2ghy
x = v_1x*t

I have attempted the problem a few times, and have posted my work below. I thought to check my work using

$v_x t = v_1 \times \cos\theta \times t = \Delta x$

to see if I get back expected results, and I did for the horizontal motion (the substitutions are from the numbered steps below):

$v_x t = v_1 \times \cos\theta \times t$
$v_x t = \left(\frac{1}{cos\theta} \Delta x \sqrt{\frac{g}{2\Delta y}} \right) \times \cos\theta \times \left( \sqrt{\frac{2\Delta y}{g}}\right)$
$v_x t = \Delta x$

But when I check my work in the vertical direction, I get the curious $\Delta y = \frac{\Delta x}{2}\tan\theta$. I expected to get back my $\Delta y = 25.0$ m (or very close to that) when I back substituted the numbers but I got $\Delta y = 27.976$ m for $\Delta x = 60.0$ and $\theta = 43^0$. The difference of almost 3 is too much of a discrepancy for me to think things are correct. Can anyone tell me what I did wrong, or am I missing something when I check my work?

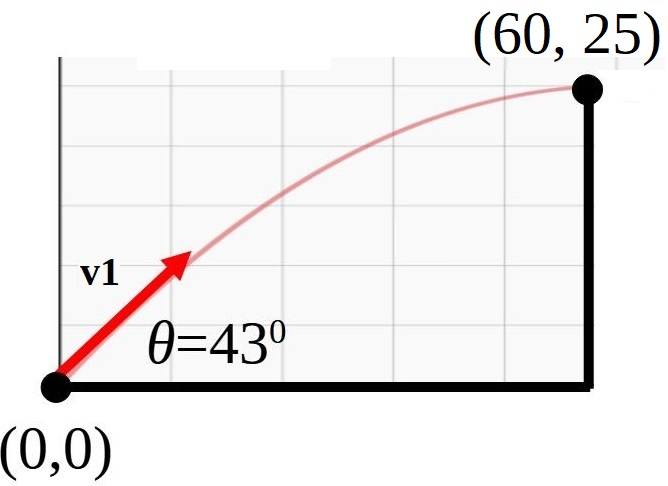
given: $\Delta y = 25.0$ m, $\Delta x = 60.0$ m, $\theta = 43^0$,
mass = $15$ kg
find: $v_1$

Get the time of flight from (0, 0) to (60, 25).

(1) $v_{2y} = v_{1y} - gt$
(2) $v_{1y} = gt$ ; we only need to clear 25.0 m, so $v_{2y} = 0.$ (and I don't have a better idea)
(3) $v_{2y}^2 = v_{1y}^2 - 2g\Delta y$
(4) $v_{1y}^2 = 2g\Delta y$ ; again we only need to clear 25.0 m, so $v_{2y} = 0.$
(5) $g^2t^2 = 2g\Delta y$ ; sub (2) into (4)
(6) $t = \sqrt{\frac{2\Delta y}{g}}$ ; solve (5) for $t$

Get the horizontal motion, $v_x$; it is constant

(7) $v_x t = \Delta x$
(8) $v_x = \Delta x / t$
(9) $v_x = \Delta x \sqrt{\frac{g}{2\Delta y}}$ ; sub (6) into (8)

Get the vertical motion $v_{1y}$

(10) $\tan\theta = \frac{v_{1y}}{v_x}$
(11) $v_{1y} = \Delta x \sqrt{\frac{g}{2\Delta y}} \tan\theta$ ; solve (10) for $v_{1y}$ and sub (9) in it

Now get $v_{1}$

(12) $v_{1}^2 = v_x^2 + v_{1y}^2$
(13) $v_{1}^2 = \Delta x^2 \frac{g}{2\Delta y} + \Delta x^2 \frac{g}{2\Delta y} \tan^2\theta$ ; sub (9) and (11) into (12)
(14) $v_{1}^2 = (1 + \tan^2\theta) \Delta x^2 \frac{g}{2\Delta y}$
(14) $v_{1} = \sec\theta \Delta x \sqrt{\frac{g}{2\Delta y}}$

$v_1 = (\sec43^0)60\left(\sqrt{\frac{9.81}{50}}\right) \approx 36.339 m/s$

 

[erobz]

Try working with the "different" relevant equations below and compare:

$$ x = v \cos \theta t $$

$$ y = v \sin \theta t - \frac{1}{2}gt^2$$

 

[Delta2]

Yes well something is weird with $\Delta y=\frac{\Delta x}{2}\tan\theta (1)$ because we can create variations of the problem where we keep $\Delta y,\Delta x$ the same and we just change the angle $\theta$, we will have to get different $v_1$ for each different $\theta$ but (1) just can't hold every time.
Nevertheless I can't figure out where exactly the derivation of (1) goes wrong...

 

[kuruman]

But when I check my work in the vertical direction, I get the curious $\Delta y = \frac{\Delta x}{2}\tan\theta$.

That "curious" result is at it should be. Here is why. There are three angles relevant to projectile motion:

1. $\theta$ = the initial angle of projection relative to the horizontal.
2. $\varphi$ = the angle that the instantaneous position vector makes relative to the horizontal. Its tangent is $\dfrac{\Delta y}{\Delta x}$.
3. $\omega$ = the angle that the instantaneous velocity vector makes relative to the horizontal.

These angles are related by$$\tan\!\varphi=\frac{1}{2}(\tan\!\theta+\tan\!\omega).$$ In this problem, you have correctly deduced that minimum initial speed means that the projectile must pass over the barrier with zero vertical component of its velocity. At that instant, $\omega = 0$ in which case the equation above becomes $$\tan\!\varphi=\frac{\Delta y}{\Delta x}=\frac{1}{2}(\tan\!\theta+0)$$ which is what you got.

The three-tangent relation can be obtained by eliminating time $t$ from the kinematic equations to get the trajectory equation and then grouping the variables appropriately. You may wish to read this insight article that shows the details of this derivation and also has other goodies about projectile motion.

 

[Delta2]

I think the angle $\theta$ for which the missile "just tops out" the cliff is unique. For this unique angle is that the (1) of my post #3 holds, for any other angle it does not hold.

 

[kuruman]

I think the angle $\theta$ for which the missile "just tops out" the cliff is unique. For this unique angle is that the (1) of my post #3 holds, for any other angle it does not hold.

I agree. The angle for just topping out is unique for a given $\Delta y$ and $\Delta x$. Here is another way of proving the relation. When the projectile "just tops out" its vertical velocity is zero. Its average vertical velocity is $\bar v_y=\frac{1}{2}v_{0y}$ and the time elapsed is $t_1=\dfrac{2\Delta y}{v_{0y}}$. The time for the projectile to go $\Delta x$ horizontally is $t_2=\dfrac{\Delta x}{v_{0x}}$. Clearly, $t_1=t_2$ in which case $$\frac{2\Delta y}{v_{0y}}=\frac{\Delta x}{v_{0x}}\implies \frac{\Delta y}{\Delta x}=\frac{1}{2}\frac{v_{0y}}{v_{0x}}=\frac{1}{2}\tan\theta.$$This works only at maximum height. If the projectile does not top out but, say, it keeps on rising, then the relation must include the tangent of angle $\omega$ and is shown in post #4.

 

[Orodruin]

In this problem, you have correctly deduced that minimum initial speed means that the projectile must pass over the barrier with zero vertical component of its velocity.

I disagree. While that is a correct result if you can vary the launch angle freely, it is not a correct result here as the launch angle is given in the problem. In fact, it will only be the case if the given angle happens to coincide with the appropriate launch angle.

 

[Delta2]

To @GreyNoise : Your mistake is that you assume that with the given angle of 43 degrees, the missile can reach the top of the cliff with zero vertical velocity. This cannot happen for this angle for any initial velocity.
The angle for which the missile can reach the top with exactly zero vertical velocity is $\theta_0=\arctan\frac{2\Delta y}{\Delta x}=39.805$

 

[kuruman]

I disagree. While that is a correct result if you can vary the launch angle freely, it is not a correct result here as the launch angle is given in the problem. In fact, it will only be the case if the given angle happens to coincide with the appropriate launch angle.

Yes, I misread the calculated tangents (0.466 for 0.4166) and thought that in this problem the angle was the appropriate launch angle.

 

[GreyNoise]

A big thnx to everyone for your help on this problem. As all of you took the time to help out, I thought to share my final solution. Shout out to kuruman for the insight article; it was the crow bar I needed to pry out an answer.

given: $\Delta y$ = 25.0 m, $\Delta x$ = 60.0 m, $m$ = 15.0 kg, $\theta$ = 43$^0$
find: $v_1$

(1) $\frac{\Delta x}{\tan\theta - \tan\varphi} = 2\frac{v_{0x}^2}{g}$, $~~~~~~~~~~$eqn (4)

(2) $\Delta x = R = \text{ (range)}$
$~~~~~\tan\varphi = \frac{\Delta y}{R}$
$~~~~~v_{0x}^2 = v_0^2\cos^2\theta$

(3) $\frac{R}{\tan\theta - \frac{\Delta y}{R}} = 2\frac{v_0^2\cos^2\theta}{g}$
(4) $v_0 = \frac{R}{\cos\theta}\sqrt{\frac{g}{2R\tan\theta-2\Delta y}}$

$~~~~~R = 60.0$ m
$~~~~~\theta = 43^0$
$~~~~~\Delta y = 25.0$
$~~~~~g = 9.81$

(5) $v_1 = \frac{60.0}{\cos43^0}\sqrt{\frac{9.81}{2\times 60.0\tan43^0-2\times 25.0}} \approx 32.6593 \frac{\text{ m}}{\text{ s}}$

Now check the work:
Time to top of flight is $t_{tof} = v_{0y}/g = v_0\sin\theta/g \approx$ 2.2075 s
Hang time or free fall time is $t_{ff} = 2\times t_{tof} \approx$ 4.5410 s
The vertical distance $\Delta y_{tof}$ at the top of flight at time $t_{tof}$ is $\Delta y_{tof} = v_{y0}^2/(2g) \approx$ 25.2860 m
Downrange distance $\Delta x_{tof}$ at top of flight at time $t_{tof}$ is $v_{0x} t_{tof} = v_0\cos\theta t_{tof} \approx$ 54.2319 m
Downrange distance $\Delta x_{ff}$ at landing is $v_{0x} t_{ff} = v_0\cos\theta t_{ff} \approx$ 108.4640 m (or simply $2\times \Delta x_{tof}$)

So the trajectory is a parabola that passes through the launch point (0,0), the top of flight point
(54.2319, 25.2860) and the landing point (0, 108.4640). It should also pass through (25, 60) if this is the solution. As can be seen in the figure below, the parabola fits quite nicely (passes very near (60, 25)), so I am satisfied that it is the solution. Thnx again everyone.

 

[Orodruin]

A big thnx to everyone for your help on this problem. As all of you took the time to help out, I thought to share my final solution. Shout out to kuruman for the insight article; it was the crow bar I needed to pry out an answer.

given: $\Delta y$ = 25.0 m, $\Delta x$ = 60.0 m, $m$ = 15.0 kg, $\theta$ = 43$^0$
find: $v_1$

(1) $\frac{\Delta x}{\tan\theta - \tan\varphi} = 2\frac{v_{0x}^2}{g}$, $~~~~~~~~~~$eqn (4)

(2) $\Delta x = R = \text{ (range)}$
$~~~~~\tan\varphi = \frac{\Delta y}{R}$
$~~~~~v_{0x}^2 = v_0^2\cos^2\theta$

(3) $\frac{R}{\tan\theta - \frac{\Delta y}{R}} = 2\frac{v_0^2\cos^2\theta}{g}$
(4) $v_0 = \frac{R}{\cos\theta}\sqrt{\frac{g}{2R\tan\theta-2\Delta y}}$

$~~~~~R = 60.0$ m
$~~~~~\theta = 43^0$
$~~~~~\Delta y = 25.0$
$~~~~~g = 9.81$

(5) $v_1 = \frac{60.0}{\cos43^0}\sqrt{\frac{9.81}{2\times 60.0\tan43^0-2\times 25.0}} \approx 32.6593 \frac{\text{ m}}{\text{ s}}$

Now check the work:
Time to top of flight is $t_{tof} = v_{0y}/g = v_0\sin\theta/g \approx$ 2.2075 s
Hang time or free fall time is $t_{ff} = 2\times t_{tof} \approx$ 4.5410 s
The vertical distance $\Delta y_{tof}$ at the top of flight at time $t_{tof}$ is $\Delta y_{tof} = v_{y0}^2/(2g) \approx$ 25.2860 m
Downrange distance $\Delta x_{tof}$ at top of flight at time $t_{tof}$ is $v_{0x} t_{tof} = v_0\cos\theta t_{tof} \approx$ 54.2319 m
Downrange distance $\Delta x_{ff}$ at landing is $v_{0x} t_{ff} = v_0\cos\theta t_{ff} \approx$ 108.4640 m (or simply $2\times \Delta x_{tof}$)

So the trajectory is a parabola that passes through the launch point (0,0), the top of flight point
(54.2319, 25.2860) and the landing point (0, 108.4640). It should also pass through (25, 60) if this is the solution. As can be seen in the figure below, the parabola fits quite nicely (passes very near (60, 25)), so I am satisfied that it is the solution. Thnx again everyone.

View attachment 303976

Now that you have a result, the most straightforward way in my book is noting that
$$
\Delta x = vt \cos\theta, \quad
\Delta y = vt \sin\theta - \frac{gt^2}{2}
$$
Inserting the first relation into the second,
$$
\Delta y = {\Delta x}\tan\theta - \frac{g \Delta x^2}{2v^2\cos^2\theta}.
$$
Solving for $v$ gives the required result.