Istiak
- 158
- 12
- Homework Statement
- Two ships are traveling parallel to each other in opposite directions with speeds v_1 and v_2 One ship fires on the other. At what angle \phi (with respect to the direction of the firing ship) should the gun be aimed at the target ship in order to make a if the shot is fired at the instant when both vessels are on the straight line perpendicular to their course? The shell velocity v_0 is assumed constant.
- Relevant Equations
- v=u+at
Question :

Solution attempt :
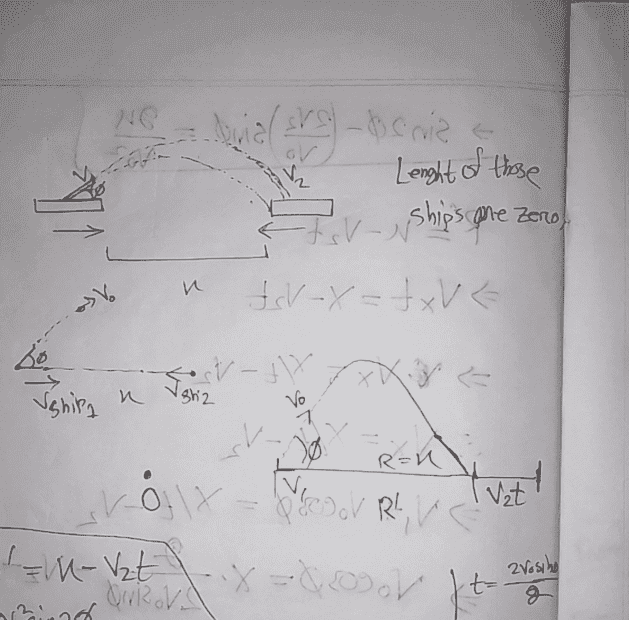
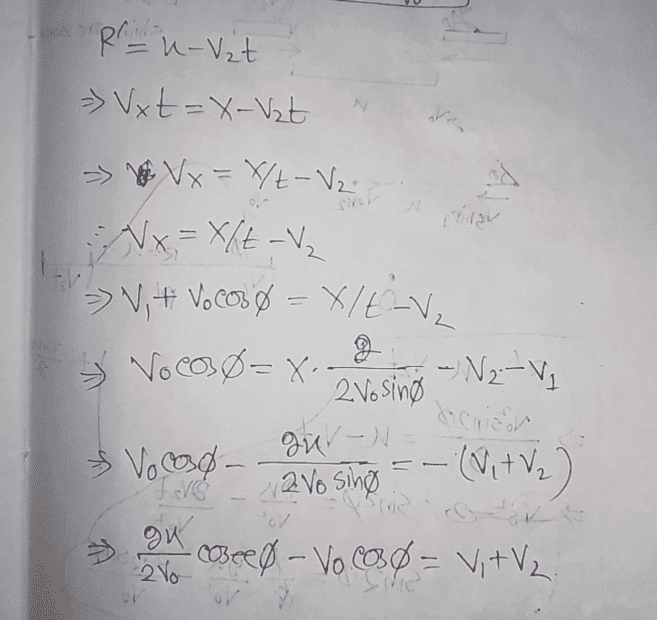
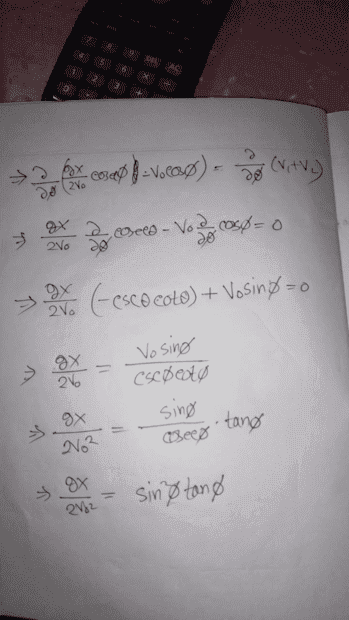
Solution attempt :