Projection postulate and the state of a system

[Kashmir]

Quantum Mechanics, McIntyre states the projection postulate as:

"After a measurement of $A$ that yields the result $a_n$,the quantum system is in a new state that is the normalized projection of the original system ket onto the ket (or kets) corresponding to the result of the measurement"

"$\left|\psi^\prime\right> = \frac{P_n\left|\psi\right>}{\sqrt{\left<\psi\right|P_n\left|\psi\right>}}.$"

Then we do a Stern Gerlach type experiment as shown in figure below (The X, Z are analyzers that measure the x, z spin of incoming stream of atoms. The up arrow is up spin.
At the right end is the final counter)

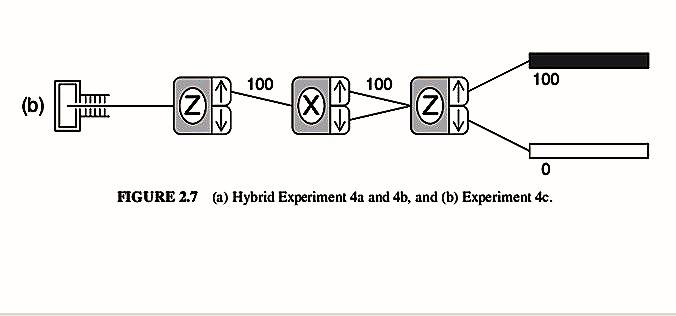
The author then says that the state of atoms input to the final Z analyzer is $\begin{aligned}\left|\psi_{2}\right\rangle &=\frac{\left(P_{+x}+P_{-x}\right)\left|\psi_{1}\right\rangle}{\sqrt{\left\langle\psi_{1}\left|\left(P_{+x}+e_{-x}\right)\right| \psi_{1}\right\rangle}} \\ &=\frac{\left(P_{+x}+P_{-x}\right)|+\rangle}{\sqrt{\left\langle+\left|\left(P_{+x}+P_{-x}\right)\right|+\right\rangle}} . \end{aligned}$ because "both states are used, the relevant projection operator is the sum of the two projection operators foreach port, $P_{+x}+P_{-x}$, where $P_{+x}=|+\rangle_{x x}\langle+$ and $P_{-x}=|-\rangle_{x x}(-\mid$"I'm not able to understand why should the state input to the final Z analyzer be $\begin{aligned}\left|\psi_{2}\right\rangle &=\frac{\left(P_{+x}+P_{-x}\right)|+\rangle}{\sqrt{\left\langle+\left|\left(P_{+x}+P_{-x}\right)\right|+\right\rangle}} . \end{aligned}$

How does this follow from the projection postulate?

 

[PeroK]

I'm not able to understand why should the state input to the final Z analyzer be $\begin{aligned}\left|\psi_{2}\right\rangle &=\frac{\left(P_{+x}+P_{-x}\right)|+\rangle}{\sqrt{\left\langle+\left|\left(P_{+x}+P_{-x}\right)\right|+\right\rangle}} . \end{aligned}$

How does this follow from the projection postulate?

What do you think it should be? What does your calculation give?

I assume McIntyre has covered the concept of superposition of states.

 

[Kashmir]

What do you think it should be? What does your calculation give?

I assume McIntyre has covered the concept of superposition of states.

McIntyre does talk about superposition states earlier. Here it is
"A general spin- $1 / 2$ state vector $|\psi\rangle$ can be expressed as a combination of the basis kets $|+\rangle$ and $|-\rangle$
$|\psi\rangle=a|+\rangle+b|-\rangle$" So basically a superposition state is not an eigenstate but a linear combination of them.

 

[PeroK]

McIntyre does talk about superposition states earlier. Here it is
"A general spin- $1 / 2$ state vector $|\psi\rangle$ can be expressed as a combination of the basis kets $|+\rangle$ and $|-\rangle$
$|\psi\rangle=a|+\rangle+b|-\rangle$" So basically a superposition state is not an eigenstate but a linear combination of them.

Okay, so what else could $|\psi_2 \rangle$ be? If it's not as above, what do you calculate it to be?

 

[Kashmir]

Okay, so what else could $|\psi_2 \rangle$ be? If it's not as above, what do you calculate it to be?

Some of the atoms will have $|+\rangle xx$and others will have $|-\rangle xx$ some will be spin up along x-axis and others spin down.

 

[PeroK]

Some of the atoms will have $|+\rangle x$and others will have $|-\rangle x$

Ah, okay. Yes, this is the heart of QM. As Feynman said, all the mysteries of QM stem from this one point.

Classically, yes, an atom would emerge from the X-system either as $x+$ or as $x-$. We might not know which, but it would definitely be one or the other.

QM says something very different. QM says that each atom emerges in a superposition of $|x+ \rangle$ and $|x- \rangle$.

In other words, classical mechanics and QM make different predictions for what would happen when we put the atoms through the second Z-system:

Classical mechanics says that the 50% of atoms that are $x+$ get split 50-50 into $z+$ and $z-$. And, so do the 50% that are $x-$. We expect, therefore, a 50-50 split coming out of the second Z-system.

QM says that the spin state that emerges from the X-system is an equal superposition of $|x+ \rangle$ and $|x- \rangle$. And, in fact, each atom is still effectively in a state of $|z+\rangle$. So, QM predicts that all the atoms will come out the second Z-system in the up direction.

In truth, this is an idealised experiment, but similar experiments have shown that QM is correct and classical mechanics fails to make the correct predictions.

This is the motivation to study QM and the states-as-complex-amplitudes formalism.

 

[PeroK]

PS does this mean that a Stern-Gerlach magnet does not actually measure the spin on the atom? Yes! The only actual measurement is when the atom is detected at the screen and the QM of spin states is inferred from that. Until it hits the screen, the atom remains in a superposition.

 

[Kashmir]

Ah, okay. Yes, this is the heart of QM. As Feynman said, all the mysteries of QM stem from this one point.

Classically, yes, an atom would emerge from the X-system either as $x+$ or as $x-$. We might not know which, but it would definitely be one or the other.

QM says something very different. QM says that each atom emerges in a superposition of $|x+ \rangle$ and $|x- \rangle$.

In other words, classical mechanics and QM make different predictions for what would happen when we put the atoms through the second Z-system:

Classical mechanics says that the 50% of atoms that are $x+$ get split 50-50 into $z+$ and $z-$. And, so do the 50% that are $x-$. We expect, therefore, a 50-50 split coming out of the second Z-system.

QM says that the spin state that emerges from the X-system is an equal superposition of $|x+ \rangle$ and $|x- \rangle$. And, in fact, each atom is still effectively in a state of $|z+\rangle$. So, QM predicts that all the atoms will come out the second Z-system in the up direction.

In truth, this is an idealised experiment, but similar experiments have shown that QM is correct and classical mechanics fails to make the correct predictions.

This is the motivation to study QM and the states-as-complex-amplitudes formalism.

Thank you,it is really surprising! . But still I'm not able to understand how the projection postulate gives me the superposition state. The author says "So we need only calculate the probability of passage through the third analyzer. The crucial step is determining the input state, for which we use the projection postulate. Since both states are used, the relevant projection operator is the sum of the two projection operators for each port, $P_{+x}+P_{-x}$ where $P_{+x}=|+\rangle_{x x}\left(+\mid\right.$ and $P_{-x}=|-\rangle_{x x}\langle-|$. Thus the state after the second analyzer is
$\begin{aligned} \left|\psi_{2}\right\rangle &=\frac{\left(P_{+x}+P_{-x}\right)\left|\psi_{1}\right\rangle}{\sqrt{\left\langle\psi_{1}\left|\left(P_{+x}+P_{-x}\right)\right| \psi_{1}\right\rangle}} . \\ &=\frac{\left(P_{+x}+P_{-x}\right)|+\rangle}{\sqrt{\left\langle+\left|\left(P_{+x}+P_{-x}\right)\right|+\right\rangle}} . \end{aligned}$ "

 

[PeroK]

Thank you,it is really surprising! . But still I'm not able to understand how the projection postulate gives me the superposition state. The author says "So we need only calculate the probability of passage through the third analyzer. The crucial step is determining the input state, for which we use the projection postulate. Since both states are used, the relevant projection operator is the sum of the two projection operators for each port, $P_{+x}+P_{-x}$ where $P_{+x}=|+\rangle_{x x}\left(+\mid\right.$ and $P_{-x}=|-\rangle_{x x}\langle-|$. Thus the state after the second analyzer is
$\begin{aligned} \left|\psi_{2}\right\rangle &=\frac{\left(P_{+x}+P_{-x}\right)\left|\psi_{1}\right\rangle}{\sqrt{\left\langle\psi_{1}\left|\left(P_{+x}+P_{-x}\right)\right| \psi_{1}\right\rangle}} . \\ &=\frac{\left(P_{+x}+P_{-x}\right)|+\rangle}{\sqrt{\left\langle+\left|\left(P_{+x}+P_{-x}\right)\right|+\right\rangle}} . \end{aligned}$ "

That's just the superposition of states written out in projection notation.

 

[Kashmir]

That's just the superposition of states written out in projection notation.

I'm not able to understand :(