Proof of a Lemma regarding absolute values

[WWCY]

Hi all,

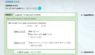
There's this proof that I've been trying to wrap my head around but it just doesn't seem to sink in. I've attached a screenshot below. Many thanks in advance!

Consider Case 1. There is a step that goes
$$\text{Then} \ |r| = r$$
$$Then -|r| \leq |r| \ \text{and} \ r \leq |r|$$
Why is this the case? This seems to imply that because $|r|=r$, then $r \leq |r|$. Is this because of the "generalisation" rule of inference that goes
$$p$$
$$\text{Therefore} \ p \vee q$$
Where $p = |r| = r$ and $q = |r| > r$? If so, why not write $q = |r| < r$ and get a completely different result altogether?

 

[nuuskur]

The lemma says $|r|\leq |r|$ which should be trivial.

For case 1 they already establish $r=|r|$ so $r\leq |r|$ holds trivially. Yes, $p\rightarrow p\lor q$ does the trick here.

You may take $q=|r|$ and then write $r=|r| \rightarrow r\leq |r| \lor |r|<r$, but $q: |r|<r$ is simply not true.