Proof Quest: Non-Equilateral Triangle Enclosing Point Z

[frusciante]

I am struggling with this question, it would be easy enough if the triangle was equilateral but that is not necessarily the case.

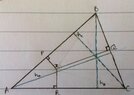
Let (ha, hb, hc) be heights in the triangle ABC, and let Z be a point inside the triangle.

Further to this, consider the points P, Q, R on the sides AB, BC and AC, respectively. P, Q, R lie such that ZP is perpendicular to AB, ZQ is perpendicular to BC, and ZR is perpendicular to AC.

Show that ha/ZQ + hb/ZR + hc/ZP >= 9.

So far I have considered;
Area(ABC) = Area(AZC) + Area(AZB) + Area(BZC) = 0,5*(AC*ZR)+0,5*(AB*ZP)+0,5*(BC*ZQ)

But I don't know if that is any useful. Any comments?

Here is a sketched form of the triangle;

View attachment 5798

https://gyazo.com/7742bc1428ac5adf84033dfc2ec29564

 

[Evgeny.Makarov]

Prove that $$\frac{ZP}{h_c}+\frac{ZQ}{h_a}+\frac{ZR}{h_b}=1$$. Then use the fact that $$(x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\ge9$$ (proved with the help of the harmonic mean).

 

[frusciante]

Prove that $$\frac{ZP}{h_c}+\frac{ZQ}{h_a}+\frac{ZR}{h_b}=1$$. Then use the fact that $$(x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\ge9$$ (proved with the help of the harmonic mean).

Thank you for your response, Evgeny. Indeed that first expression (=1) must hold, but I am having a hard time to prove that $$\frac{ZP}{h_c}+\frac{ZQ}{h_a}+\frac{ZR}{h_b}=1$$ since the two "types" of distances (ZP - h_c etc) aren't parallel given that the triangle is not equilateral. Any idea?

 

[Evgeny.Makarov]

I am having a hard time to prove that $$\frac{ZP}{h_c}+\frac{ZQ}{h_a}+\frac{ZR}{h_b}=1$$ since the two "types" of distances (ZP - h_c etc) aren't parallel given that the triangle is not equilateral. Any idea?

I am not sure what you mean by parallel types of distances. The altitude from $C$ and $ZP$ are parallel since they are both perpendicular to $AB$. I suggest multiplying both $h_c$ and $ZP$ by $AB$ and using your observation about the sum of areas.