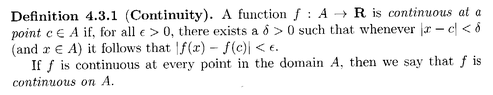SUMMARY
The function f(x) = Arcsin x is continuous on the interval [-1, 1]. According to Stephen Abbott's "Understanding Analysis," a function is continuous at a point if for every ε > 0, there exists a δ > 0 such that if |x - c| < δ, then |Arcsin x - Arcsin c| < ε. This definition establishes the framework for proving the continuity of the Arcsin function within the specified interval. The discussion emphasizes the importance of understanding the definitions and properties of continuous functions.
PREREQUISITES
- Understanding of the definition of continuous functions from real analysis.
- Familiarity with the properties of inverse functions.
- Knowledge of the function Arcsin and its domain.
- Basic proficiency in mathematical proofs and ε-δ definitions.
NEXT STEPS
- Study the ε-δ definition of continuity in more depth.
- Explore the properties of inverse functions and their continuity.
- Review Theorem 4.3.2 from Stephen Abbott's "Understanding Analysis."
- Practice proving the continuity of other functions using similar methods.
USEFUL FOR
Students of real analysis, mathematicians, and educators looking to deepen their understanding of continuity and inverse functions in calculus.