- #1
imiyakawa
- 262
- 1
Homework Statement
If;
a*x + b*y = c*x + d*y
x ≠ y
a,b,c,d ≥ 0
Prove that;
a=c
b=d
2. The attempt at a solution
I've been fiddling with this equation and have been getting nowhere.
imiyakawa said:Homework Statement
If;
a*x + b*y = c*x + d*y
x ≠ y
a,b,c,d ≥ 0
Prove that;
a=c
b=d
2. The attempt at a solution
I've been fiddling with this equation and have been getting nowhere.
imiyakawa said:x ≠ y
imiyakawa said:Homework Statement
If;
a*x + b*y = c*x + d*y
x ≠ y
a,b,c,d ≥ 0
Prove that;
a=c
b=d
2. The attempt at a solution
I've been fiddling with this equation and have been getting nowhere.
imiyakawa said:Hi, thank you for your suggestion. Are you sure that this is a proof? I'm not sure;
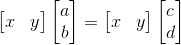
[x y] = [x y], hence
[a b] = [c d], hence
a=c,
b=dI mean it makes complete sense but it's a part of a much longer proof for an assignment so it's important that it's correct
Mathoholic! said:Your matricial equation is wrong, you can only multiply matrices like so: (mxn)(nxp); meaning that the first matrix has to have the number of columns equal to the number of lines of the second matrix (n), and the resultant matrix will be (mxp). And so:
ax+by=cx+dy → (1x2).(2x2)=(1x2).(2x2)=(1x2)
The x and y in the 1 by 2 matrices and a,b,c, and d in the 2 by 2 diagonal matrix. If you compute it, you'll have the following:
(ax,by)=(cx,dy) → ax=cx [itex]\wedge[/itex] by=dy
From those equations you conclude that a=c and that b=d.
Ray Vickson said:That conclusion is wrong: the example I gave before (2*x + y = x + 3*y) is a counterexample: this has solutions x ≠ y, but we do NOT have 2 = 1, and/or 1 = 3.
RGV
I disagree. we don't even know what the equation means at this point, and the OP has never cleared this up. IOW, we don't know whether the equation is conditionally true or identically true.Mathoholic! said:I've just proved it isn't wrong, how can you say it is? You're misinterpreting the problem, or... perhaps we're tackling it differently.
This equational problem is about the same expression but with different coeficients (alphabetically, at least). Algebraically, I've proved it (for x≠0 and y≠0). For two different expressions:
ax+by=cx+dy
It's obvious that it's not right as a could be a different number then c and the same for b and d. However, in algebra, such is equation is correct because we're only interested to prove it's equal and what it means to be equal (a=c and b=d).
Algebraically, the meaning of the equation is fundamental.
Mathoholic! said:Now, I'm not going to say you're wrong (you aren't, you're only facing it in another point of view, maybe geometrically, with a independent of c and b independent of d, as two separate expressions).
Let me know what you think..
tiny-tim said:do you mean x is not parallel to y ?
sjb-2812 said:For instance: (8 x 9) + (7 x 4) = (5 x 2) + (30 x 3)
Mathoholic! said:Your matricial equation is wrong, you can only multiply matrices like so: (mxn)(nxp); meaning that the first matrix has to have the number of columns equal to the number of lines of the second matrix (n), and the resultant matrix will be (mxp). And so:
ax+by=cx+dy → (1x2).(2x2)=(1x2).(2x2)=(1x2)
The x and y in the 1 by 2 matrices and a,b,c, and d in the 2 by 2 diagonal matrix. If you compute it, you'll have the following:
(ax,by)=(cx,dy) → ax=cx [itex]\wedge[/itex] by=dy
From those equations you conclude that a=c and that b=d.
imiyakawa said:Sorry, x and y are just real numbers. Such as -12.12, 20, 5080.892, etc.
This is not of the form (a)x + (b)y = (c)x + (d)y
Unfortunately I still don't see what's wrong with the matrix that I typed up. Not that you're wrong, I just can't understand what you're saying because my maths education is at quite a low level.
I multiplied a (1*2) matrix with a (2*1) matrix to represent a*x + b*y. Is there something wrong with this?
Ray Vickson said:Whether or not the statement you want to prove is true or false depends on *exactly* what your question meant, which was not obvious from what you wrote. Did you mean to say "for all x ≠ y"? If so, your statement is true and very easy to prove. If you did not mean for all x≠y (but just for some solution with x ≠ y) then the statement is false. Only YOU really know what you meant.
RGV
imiyakawa said:Unfortunately I still don't see what's wrong with the matrix that I typed up. Not that you're wrong, I just can't understand what you're saying because my maths education is at quite a low level.
I multiplied a (1*2) matrix with a (2*1) matrix to represent a*x + b*y. Is there something wrong with this?
In mathematics, LHS stands for "Left Hand Side" and RHS stands for "Right Hand Side". These terms refer to the two sides of an equation, with the equal sign in between.
The coefficients on the left and right sides of an equation have to be equal because of the fundamental property of equality in mathematics. This means that whatever operation is performed on one side of the equation must also be performed on the other side in order to maintain the balance and equality of the equation.
No, the LHS and RHS coefficients cannot be different. If they were, it would result in an unbalanced equation and would not be a true statement.
There are no exceptions to this rule. It applies to all equations, regardless of the variables or operations involved.
In chemistry, the Law of Conservation of Mass states that matter cannot be created or destroyed in a chemical reaction. This is similar to the concept of LHS and RHS coefficients being equal in an equation. It ensures that the amount of matter on both sides of the reaction remains balanced and constant.