- #1
vcsharp2003
- 897
- 176
- Homework Statement
- I am unable to see why elementary row operations or elementary column operations can be done to both sides of a matrix equation in the manner explained in my textbook. It doesn't make sense to me. In my textbook it says the following.
"Let X, A and B be matrices of, the same order such that X = AB. In order to apply a sequence of elementary row operations on the matrix equation X = AB, we will apply these row operations simultaneously on X and on the first matrix A of the product AB on RHS.
Similarly, in order to apply a sequence of elementary column operations on the matrix equation X = AB, we will apply, these operations simultaneously on X and on the second matrix B of the product AB on RHS."
- Relevant Equations
- None
I feel if we have the matrix equation X = AB, where X,A and B are matrices of the same order, then if we apply an elementary row operation to X on LHS, then we must apply the same elementary row operation to the matrix C = AB on the RHS and this makes sense to me. But the book says, that we don't need to apply the same row operation to the whole matrix AB on RHS, but instead only to A. I am at a complete loss to explain this.
An example given in the book is as below. My problem is why the mentioned row operation is only applied to the first matrix on RHS and not to the whole matrix resulting from multiplication of two matrices on RHS. According to simple logic, the same row operation used on LHS should have been used for the single matrix that is the result of IA i.e. for matrix C = IA, where I is the identity matrix.
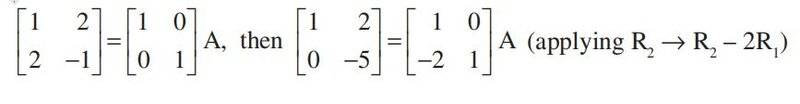
An example given in the book is as below. My problem is why the mentioned row operation is only applied to the first matrix on RHS and not to the whole matrix resulting from multiplication of two matrices on RHS. According to simple logic, the same row operation used on LHS should have been used for the single matrix that is the result of IA i.e. for matrix C = IA, where I is the identity matrix.
Last edited: