SUMMARY
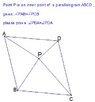
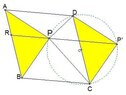
The discussion focuses on proving that the angles $\angle PBA$ and $\angle PDA$ are equal in a parallelogram ABCD, given that point P is an interior point with $\angle PAB = \angle PCB$. By constructing lines P'C parallel to PB and P'P parallel to BC, two parallelograms, BCP'P and APP'D, are formed. The cyclic nature of points C, P'D, and P leads to the conclusion that $\angle DPP' = \angle DCP'$, which directly establishes the equality $\angle PBA = \angle PDA$.
PREREQUISITES
- Understanding of basic properties of parallelograms
- Knowledge of cyclic quadrilaterals
- Familiarity with angle relationships in geometry
- Ability to construct geometric figures and parallel lines
NEXT STEPS
- Study the properties of cyclic quadrilaterals in depth
- Explore the implications of angle chasing in geometric proofs
- Learn about the construction of parallel lines in Euclidean geometry
- Investigate theorems related to angles in parallelograms
USEFUL FOR
Geometry students, mathematics educators, and anyone interested in geometric proofs and properties of parallelograms.