Prove that center of DG = center of the red circle.

  • Context: MHB 
  • Thread starter Thread starter maxkor
  • Start date Start date
  • Tags Tags
    Center Circle
Click For Summary
SUMMARY

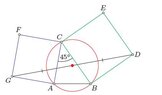
The discussion focuses on proving that the center of segment DG is equivalent to the center of the red circle formed by the intersection of extended lines from squares BCED and ACFG. Key steps include extending line FC to intersect point D, extending line EC to intersect point G, and demonstrating that the intersection of lines GA and DB at point X lies on the red circle, with CX serving as its diameter. Additionally, it is established that quadrilateral CDXG is a parallelogram, confirming that its diagonals intersect at the circle's center.

PREREQUISITES
  • Understanding of geometric properties of squares
  • Knowledge of circle geometry, specifically diameters and centers
  • Familiarity with properties of parallelograms
  • Ability to construct geometric proofs
NEXT STEPS
  • Study the properties of squares and their diagonals
  • Learn about circle geometry, focusing on diameters and centers
  • Explore the characteristics of parallelograms and their diagonal properties
  • Practice constructing geometric proofs using extended lines and intersections
USEFUL FOR

Students of geometry, mathematics educators, and anyone interested in geometric proofs and properties of shapes.

maxkor
Messages
79
Reaction score
0
Let BCED and ACFG square. Prove that center of DG = center of the red circle.

View attachment 6025

I don't know how to start
 

Attachments

  • a.JPG
    a.JPG
    8.5 KB · Views: 111
Last edited:
Mathematics news on Phys.org
maxkor said:
Let BCED and ACFG square. Prove that center of DG = center of the red circle.
I don't know how to start
Extend some of the lines in the figure.

• Show that if you extend the line FC then it passes through D.

• Show that if you extend the line EC then it passes through G.

• Show that if you extend the lines GA and DB to meet at X then X lies on the red circle, and CX is a diameter of the circle.

• Show that CDXG is a parallelogram whose diagonals meet at the centre of the circle.
 

Similar threads

High School Circle tangent to two lines and another circle
  • · Replies 2 ·
Replies
2
Views
4K
MHB Finding the Center of a Circle
  • · Replies 3 ·
Replies
3
Views
1K
High School Calculate distance between ends of a circle segment
  • · Replies 22 ·
Replies
22
Views
3K
MHB Find the area of the shaded region
  • · Replies 2 ·
Replies
2
Views
1K
MHB [ASK] A Line Intercepting A Circle
  • · Replies 4 ·
Replies
4
Views
1K
MHB Adam's Circles: Splitting & Connecting Segments
  • · Replies 6 ·
Replies
6
Views
1K
MHB Finding the Equation of a Tangent Circle with Center (3,5)
  • · Replies 2 ·
Replies
2
Views
2K
High School How to find a length of a "radius" not centered in a circle?
  • · Replies 2 ·
Replies
2
Views
2K
MHB Can Three Circles Intersect at a Common Point?
  • · Replies 1 ·
Replies
1
Views
2K
MHB How Do You Find the Equation of a Line Through a Point and a Circle's Center?
  • · Replies 2 ·
Replies
2
Views
2K