SUMMARY
The difference of x^3 + y and y^3 + x is always a multiple of 6 for any integers x and y. The proof involves rewriting the expression as x(x - 1)(x + 1) - y(y - 1)(y + 1), which represents the difference of two products of three consecutive integers. Since the product of three consecutive integers is divisible by 6, the difference of such products is also divisible by 6. This can be established through mathematical induction or by analyzing the properties of consecutive integers.
PREREQUISITES
- Understanding of polynomial expressions and factorizations
- Knowledge of properties of integers and divisibility
- Familiarity with mathematical induction
- Basic concepts of triangular numbers
NEXT STEPS
- Study the principles of mathematical induction in depth
- Explore the properties of triangular numbers and their applications
- Learn about divisibility rules for integers, particularly for products
- Investigate proofs involving consecutive integers and their properties
USEFUL FOR
Mathematicians, educators, students studying number theory, and anyone interested in proofs involving integer properties and divisibility.
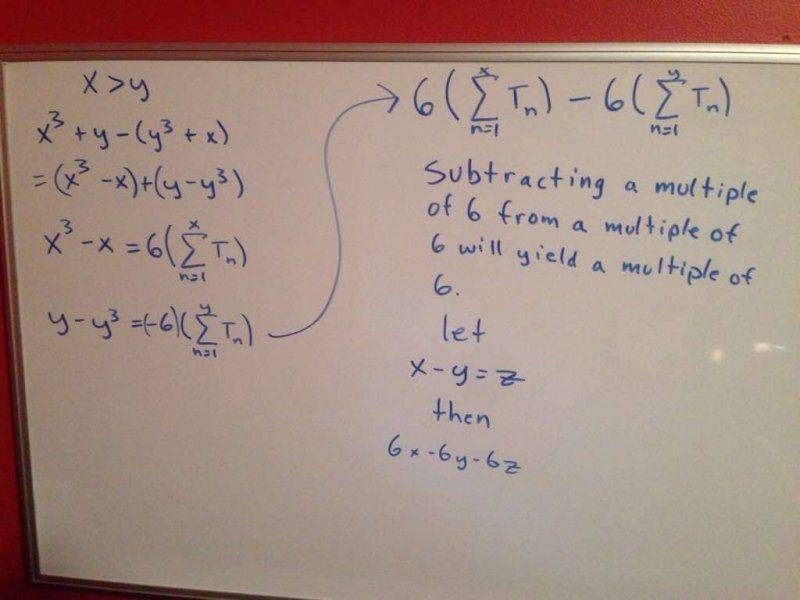 this is with the first triangular number being 0 and Tsubn being the nth triangular number.
this is with the first triangular number being 0 and Tsubn being the nth triangular number.