lfdahl
Gold Member
MHB
- 747
- 0
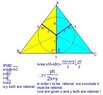
Let $\bigtriangleup$ be an isosceles triangle for which the length of a side and the length of the base are rational. Prove that the radius of the incircle of $\bigtriangleup $ is rational if and only if the two right triangles formed by the altitude to the base are similar to a right triangle with integer side lengths