SUMMARY
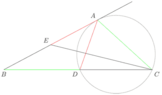
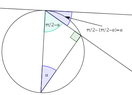
The discussion focuses on proving that the angles $\sphericalangle BAD$ and $\sphericalangle CEA$ are equal in triangle $ABC$ with specific conditions: $BD=AC$, $AD=AE$, and $AB^2=AC \cdot BC$. The proof involves demonstrating that line $AB$ is tangent to the circumcircle of triangle $ACD$ and establishing the congruence of triangles $BAD$ and $CEA$. Key relationships derived include the similarity of triangles $ABD$ and $CBA$, leading to the conclusion that $\sphericalangle BAD = \sphericalangle CEA$.
PREREQUISITES
- Understanding of triangle congruence and similarity
- Familiarity with circle theorems, particularly tangents and circumcircles
- Knowledge of angle relationships in triangles
- Basic algebraic manipulation of geometric relationships
NEXT STEPS
- Study the properties of tangents to circles, specifically the tangent-secant theorem
- Learn about triangle congruence criteria, including SAS and SSS
- Explore the concept of circumcircles and their properties in triangle geometry
- Investigate the relationships between angles in similar triangles
USEFUL FOR
Students in geometry classes, mathematics educators, and anyone interested in advanced triangle properties and proofs.