MHB Prove Triangle Inscribed in Semicircle Is Right Angle | Arundev Answers

[MarkFL]

Here is the question:

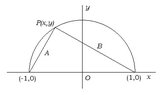
Using coordinate geometry prove that angle in a semicircle is a right angle?

I have posted a link there to this thread so the OP can view my work.

 

[MarkFL]

Hello Arundev,

Consider the following diagram:

https://www.physicsforums.com/attachments/1763._xfImport

Without loss of generality, I have chosen a unit semicircle whose center is at the origin.

Point $P$ is $$(x,y)=\left(x,\sqrt{1-x^2} \right)$$.

The slope of line segment $A$ is:

$$m_A=\frac{\sqrt{1-x^2}-0}{x-(-1)}=\frac{\sqrt{1-x^2}}{1+x}=\sqrt{\frac{1-x}{1+x}}$$

The slope of line segment $B$ is:

$$m_B=\frac{\sqrt{1-x^2}-0}{x-1}=-\frac{\sqrt{1-x^2}}{1-x}=-\sqrt{\frac{1+x}{1-x}}$$

As proven http://mathhelpboards.com/math-notes-49/perpendicular-lines-product-their-slopes-2953.html, two lines are perpendicular if the prodict of their slopes is $-1$.

$$m_Am_B=\left(\sqrt{\frac{1-x}{1+x}} \right)\left(-\sqrt{\frac{1+x}{1-x}} \right)=-1$$

Thus, we know line segments $A$ and $B$ are perpendicular, and so the triangle is a right triangle.