Proving Acute Angles from Two Equations

[Saptarshi Sarkar]

Homework Statement

A body 'A' of mass 2m collides with a body 'B' of mass m initially at rest in the Laboratory frame. The two bodies are seen to fly off at angles 'a' and 'b' respectively with respect to the incident direction. Find whether the angles a and b acute or obtuse.

Relevant Equations

$p_{x_{initial}} = p_{x_{final}}$
$p_{y_{initial}} = p_{y_{final}}$

From the above two equations, I get :

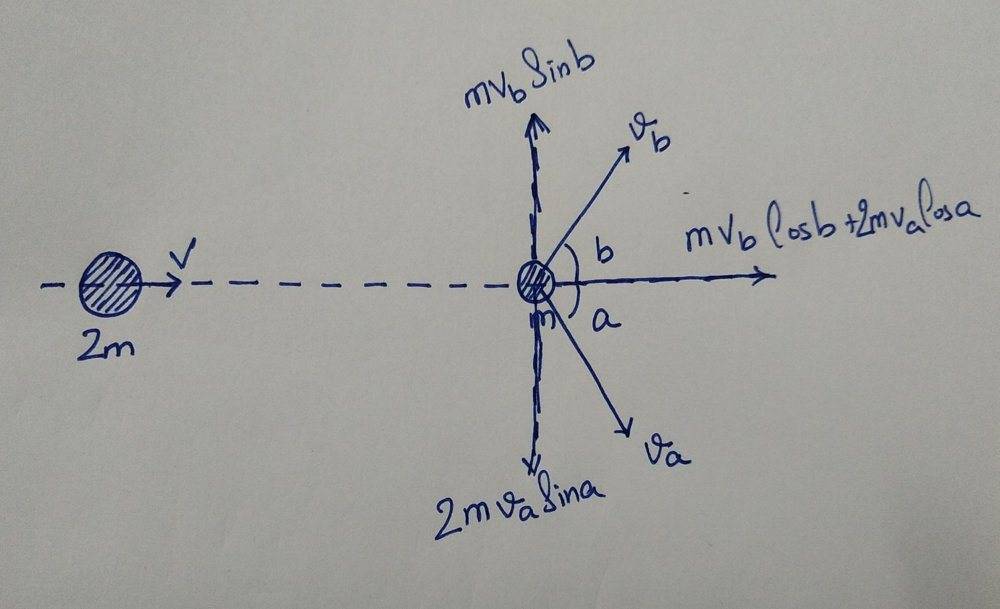
$2mv = 2mv_aCos(a) + mv_bCos(b)$
$0 = 2mv_aSin(a) - mv_bSin(b)$

But, I can't figure out how to prove how the angles should be. I think both the angles should be acute, but don't know how to show it.

 

[etotheipi]

Do we know if the collision is elastic?

 

[Saptarshi Sarkar]

Do we know if the collision is elastic?

The question does not specify it. But it's not inelastic as we can see that after the collision, both the particles remain separate.

 

[etotheipi]

The question does not specify it, but it's not inelastic as we can see that after the collision, both the particles remain separate.

It can still be inelastic if the particles remain separate, it just won't be totally inelastic.

If the collision is elastic, we can transform into the ZMF (by, in this case, subtracting $\frac{2v}{3}$ from all of our velocities before the collision). This would allow us to easily see that after the collision, in the ZMF, the particle of mass $2m$ moves away at some angle at $\frac{v}{3}$ and the particle of mass $m$ moves in exactly the opposite direction at $\frac{2v}{3}$. From this point, we can add on the ZMF velocity vector of magnitude $\frac{2v}{3}$ again and see if we can solve for the angles.

 

[haruspex]

Without info on elasticity, what can you say about KE before and after?
What inequality can you write?

 

[neilparker62]

I think somewhere there's a result which gives the maximum possible angle of deflection of the larger mass as arcsin(m/M). On this basis your angles would both be acute.

https://www.feynmanlectures.caltech.edu/info/exercises/maximum_angle_deflection.html

 

[haruspex]

It can still be inelastic if the particles remain separate, it just won't be totally inelastic.

Even if the particles do not stay together, a glancing blow can be completely inelastic. Complete inelasticity just means there is a maximal loss of KE subject to other constraints. If there's no glue or friction then the momentum of the incoming particle in a direction parallel to the plane of contact is unaffected.

I think it is reasonably obvious that maximal deflection of the incoming particle occurs when the collision is perfectly elastic.

 

[etotheipi]

Even if the particles do not stay together, a glancing blow can be completely inelastic. Complete inelasticity just means there is a maximal loss of KE subject to other constraints. If there's no glue or friction then the momentum of the incoming particle in a direction parallel to the plane of contact is unaffected.

I didn't know this, thanks for enlightening me!

I think it is reasonably obvious that maximal deflection of the incoming particle occurs when the collision is perfectly elastic.

I believe that when I scribbled down the elastic version a few days ago both angles were necessarily acute. So the inequality follows...

 

[neilparker62]

Deleted post #9 - it's incorrect. See this thread:

https://www.physicsforums.com/threads/angle-of-maximum-deflection.983227