SUMMARY
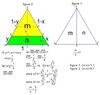
The discussion centers on proving the area ratio of two segments, \(A_1\) and \(A_2\), formed by a line dividing an equilateral triangle with equal perimeters. The established conclusion is that the ratio satisfies the inequality \(\frac{7}{9} \leq \frac{A_1}{A_2} \leq \frac{9}{7}\). Participants, including Vishal Lama from Southern Utah University, contributed various methods to demonstrate this geometric property, reinforcing the relationship between perimeter and area in equilateral triangles.
PREREQUISITES
- Understanding of equilateral triangle properties
- Familiarity with geometric inequalities
- Basic knowledge of area calculations
- Experience with mathematical proofs
NEXT STEPS
- Study geometric inequalities in triangle geometry
- Explore advanced properties of equilateral triangles
- Learn about mathematical proof techniques in geometry
- Investigate applications of perimeter-area relationships in other geometric shapes
USEFUL FOR
Mathematicians, geometry enthusiasts, educators, and students seeking to deepen their understanding of geometric properties and inequalities related to equilateral triangles.