odolwa99
- 85
- 0
In the final proof, I have \frac{h-h\tan B}{\tan B}, rather than \frac{h-h\tan B}{1+\tan B}. Can anyone help me out?
Many thanks.
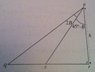
In the triangle pqr (see attachment), |\angle qrp|=90^{\circ} & |rp| = h. s is a point on [qr] such that |\angle spq|=2B & |\angle rps|=45^{\circ}-B, 0^{\circ}<B<45^{\circ}. Show that |sr|=h \tan(45^{\circ}-B)
h\tan(45-B)=h(\frac{\tan45-\tan B}{1+ tan45\cdot\tan B})=\frac{h-h\tan B}{1+\tan B}
Apply the sine rule: \frac{\sin(45-B)}{|sr|}=\frac{\sin(180-(90+45-B))}{h}
h(\sin(45-B))=|sr|\sin(45+B)
h(\sin\cos B-\cos45\sin B)=|sr|(\sin45\cos B+\cos45\sin B)
h(\frac{\cos B}{\sqrt{2}}-frac{sin B}{\sqrt{2}})=|sr|(\frac{\cos B}{\sqrt{2}}+\frac{\sin B}{\sqrt{2}})
|sr|=(\frac{h\cos B-h\sin B}{\sqrt{2}})/(\frac{\cos B}{\sin B}{\sqrt{2}})
\frac{h\sqrt{2}(\cos B- \sin B)}{\sqrt{2}(\cos B+\sin B})
h(\frac{\sin B}{\cos B}+\frac{\cos B}{\sin B})
h(-\tan B+\frac{1}{\tan B})
\frac{h-h\tan B}{\tan B}
Many thanks.
Homework Statement
In the triangle pqr (see attachment), |\angle qrp|=90^{\circ} & |rp| = h. s is a point on [qr] such that |\angle spq|=2B & |\angle rps|=45^{\circ}-B, 0^{\circ}<B<45^{\circ}. Show that |sr|=h \tan(45^{\circ}-B)
Homework Equations
The Attempt at a Solution
h\tan(45-B)=h(\frac{\tan45-\tan B}{1+ tan45\cdot\tan B})=\frac{h-h\tan B}{1+\tan B}
Apply the sine rule: \frac{\sin(45-B)}{|sr|}=\frac{\sin(180-(90+45-B))}{h}
h(\sin(45-B))=|sr|\sin(45+B)
h(\sin\cos B-\cos45\sin B)=|sr|(\sin45\cos B+\cos45\sin B)
h(\frac{\cos B}{\sqrt{2}}-frac{sin B}{\sqrt{2}})=|sr|(\frac{\cos B}{\sqrt{2}}+\frac{\sin B}{\sqrt{2}})
|sr|=(\frac{h\cos B-h\sin B}{\sqrt{2}})/(\frac{\cos B}{\sin B}{\sqrt{2}})
\frac{h\sqrt{2}(\cos B- \sin B)}{\sqrt{2}(\cos B+\sin B})
h(\frac{\sin B}{\cos B}+\frac{\cos B}{\sin B})
h(-\tan B+\frac{1}{\tan B})
\frac{h-h\tan B}{\tan B}