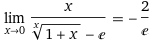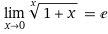Homework Help Overview
The discussion revolves around proving a limit involving the expression \( (1+x)^{1/x} \) as \( x \) approaches 0. Participants explore the nature of this limit and its relation to derivatives and logarithmic differentiation.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Assumption checking
Approaches and Questions Raised
- Participants discuss using derivatives and L'Hopital's rule to evaluate the limit. There are attempts to apply logarithmic differentiation and Taylor series expansions. Some participants question the validity of substituting \( (1+x)^{1/x} \) directly with \( e \) and explore the implications of indeterminate forms.
Discussion Status
The discussion is active, with various approaches being explored. Some participants have provided insights into using Taylor series and binomial expansions, while others are questioning assumptions and the validity of certain methods. There is no explicit consensus on a single approach, but several productive lines of reasoning are being developed.
Contextual Notes
Participants note the presence of indeterminate forms such as \( \frac{0}{0} \) and the need to investigate the behavior of functions as \( x \) approaches 0. There are also references to specific mathematical identities and expansions that may aid in resolving the limit.