SUMMARY
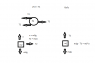
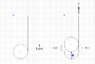
The discussion focuses on understanding the relationship between the movements of two masses, m1 and m2, connected by a pulley system. It is established that m2 moves twice the distance of m1, leading to the conclusion that the acceleration of m2 is also twice that of m1, expressed mathematically as 2a1 = a2. Participants emphasize the importance of drawing free body diagrams (FBD) for each mass to visualize the forces and relationships involved. The discussion highlights that once a displacement relationship is established, it directly influences the corresponding velocity and acceleration relationships.
PREREQUISITES
- Understanding of free body diagrams (FBD)
- Basic principles of mechanics and forces
- Knowledge of kinematic relationships in pulley systems
- Ability to differentiate equations to find velocity and acceleration relationships
NEXT STEPS
- Study the principles of kinematics in pulley systems
- Learn how to construct and analyze free body diagrams for complex systems
- Explore the differentiation of displacement equations to derive velocity and acceleration
- Research related rates in mechanics and their applications
USEFUL FOR
Students studying physics, particularly those focusing on mechanics, as well as educators looking for effective ways to explain pulley systems and related kinematic concepts.