QCD: Asymptotic not-exactly freedom?

[nikkkom]

"The strong coupling from a nonperturbative determination of the Λ parameter in three-flavor QCD"
https://arxiv.org/pdf/1706.03821.pdf
https://arxiv.org/pdf/1706.03821.pdf
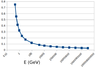
Their calculation gives strong coupling constant g^2/4pi ~= 0.08523 at 1.508 TeV. Small, but not tending to zero.

Lattice calculations seem to converge on strong coupling constant not going to zero as energy goes to infinity, but going to a small nonzero value.

Does it mean that quarks are not completely asymptotically free, they do interact even as distance goes to zero, just rather weakly?

 

[Dr.AbeNikIanEdL]

Why do you say it is not tending towards zero? It is $0.118$ at the Z mass and then the $0.085$ you quoted for $1.5$ TeV. This is also value you get perturbatively for this energy (starting from the Z mass value), and I think this is even what they are doing. Do they somewhere show something for the limit of infinite energy that ?

 

[Vanadium 50]

Does it mean that quarks are not completely asymptotically free, they do interact even as distance goes to zero, just rather weakly?

You can't get to infinite energy transferred because there is only a finite amount of energy in the visible universe.

 

[mfb]

You can't get to infinite energy transferred because there is only a finite amount of energy in the visible universe.

In addition, the SM is not valid up to the total energy in the observable universe.

 

[nikkkom]

Why do you say it is not tending towards zero? It is $0.118$ at the Z mass and then the $0.085$ you quoted for $1.5$ TeV.

That's quite modest decrease from EW breaking scale to x15 times EW breaking scale. These energies correspond to something like one thousandth of the size of proton. Before I read results like this one, I thought that asymptotic freedom should be approached even before this small scale. "Bag model" of hadrons, for example, was based on the approximation of quarks being quasi-free inside hadrons.

 

[Dr.AbeNikIanEdL]

That's quite modest decrease from EW breaking scale to x15 times EW breaking scale. These energies correspond to something like one thousandth of the size of proton. Before I read results like this one, I thought that asymptotic freedom should be approached even before this small scale.

But you would not expect to have exactly zero coupling for any finite energy anyway, do you? It is of the same order as the electroweak couplings only at the GUT scale, still $10^{13}$ or something like this higher. So what exactly do you mean by "approach asymptotic freedom"? It is formally happening at infinite energies, and $1.5$ TeV is not infinity.

As I said, this is also not specific to lattice QCD calculations, this slow running of the strong coupling is purely perturbation theory. So I think the answer to the original question is, yes there is a non-zero interaction for quarks for any finite energy, and due to the slow running it will probably not be negligible for any energy that we can reach (or as others pointed out, where QCD is probably valid). However, the statement that the strong coupling is approaching zero for infinite energy (or zero distance) is of course correct.

Also, I guess it can't be correct that quarks are just free inside hadrons, otherwise there should be no sea-quark or gluon pdfs. I guess this just shows the limitations of these models...

 

[mfb]

That's quite modest decrease from EW breaking scale to x15 times EW breaking scale. These energies correspond to something like one thousandth of the size of proton. Before I read results like this one, I thought that asymptotic freedom should be approached even before this small scale. "Bag model" of hadrons, for example, was based on the approximation of quarks being quasi-free inside hadrons.

Just a matter of plotting.