Amblambert
- 1
- 1
- Homework Statement
- For the particle in a box, sketch ψn(x) and ψn2(x) for n = 5. Is ψn(x) an eigenfunction of the momentum operator?
If the state of the system is ψn, what is the probability of finding the particle in the
left quarter of the box between 0 and L/4? What happens when n is large?
- Relevant Equations
- ψn = sqrt(2/l) sin (npix/l)
Here is my attempt at a solution. The thing I am not sure about is the final result of the Shrodinger equation and the n-values that are offered?
Did I make a math mistake?
Thank you so much for reading through this!

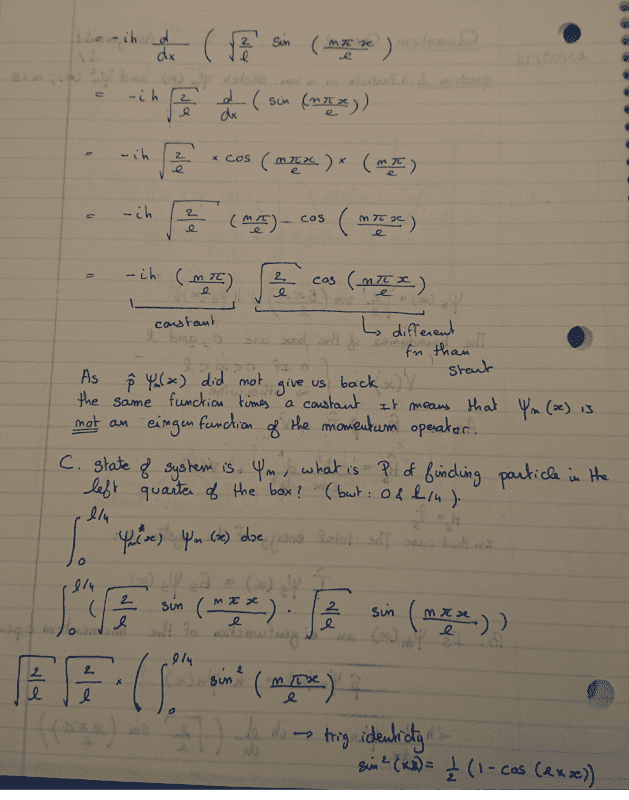
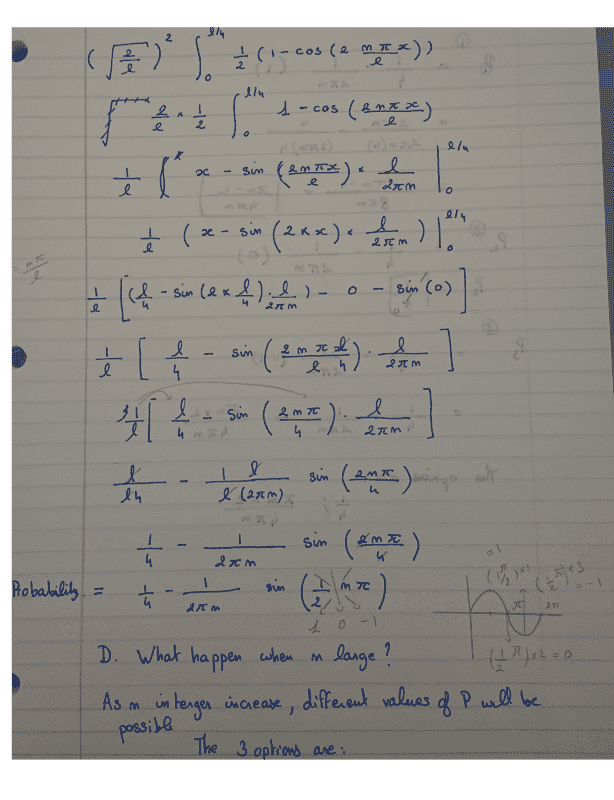
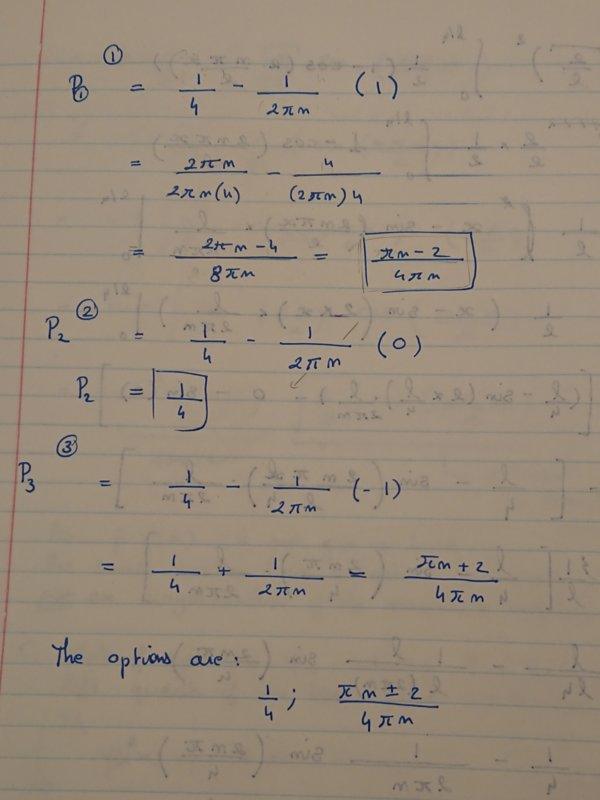
Did I make a math mistake?
Thank you so much for reading through this!