Quantum Chemistry: Theory based questions

[pmd28]

Hey all, I want to preface this with I wasn't sure if I should put this in the physics thread since it is quantum mechanics or in chemistry thread since this is for my Physical Chemistry course. I will gladly move the thread if the community feels it is more appropriate in the physics thread. I also am not aware of any equation editors as I am a returning member from a long time ago, the update is new to me.

There are three conceptual questions I attempted as practice and they are as follows:

1. Does bond length of a real molecule depend on its energy? Answer this question by referring to Figure 7.7. The bond length is the midpoint of the horizontal line connecting the two parts of V(x). (I'm assuming the two parts are split when y=0; the left and right being the separate parts)

2.The zero point energy of the particle in the box goes to zero as the length of the box approaches infinity. What is the appropriate analogue for the quantum harmonic oscillator?

3. What is the degeneracy of the energy levels for the rigid rotor in 2D? If it is not 1, explain why?My attempted solutions are the following:

1. Figure 7.7

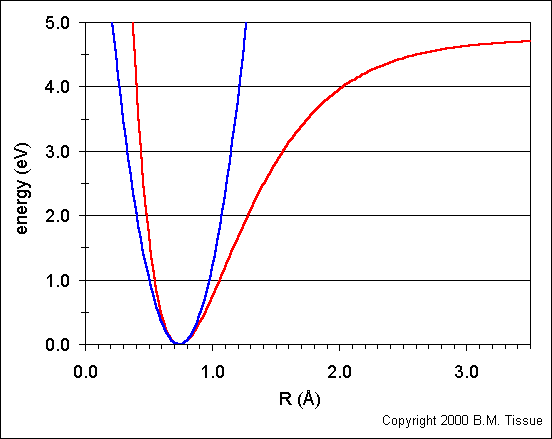
Bond length does depend on energy. As energy increases the midpoint of the horizontal moves farther to the right. (Could someone elaborate why this happens, we didn't discuss the anharmonic oscillator in too much depth during lecture)

2. E_n=h(n+1/2)(√k/μ). The equivalent scenario would be if k were to approach 0 or μ approach infinity. (Neither of these solutions seem very plausible physically, but I guess it's a model so we could assume hypothetical molecules which have infinitely heavy molecules or infinitely small force constants. Could some one address this?)

3. Since energies of the 2D rigid rotor are E_ml=((h²)(m_l²))/(2I) and m_l= 0,±1,±2,... the degeneracy would be two for all m_l except m_l=0, in which case it would be 1. (I thought if there aren't two energetically equivalent energy levels then it's termed to have "no degeneracy").

I believe my answers are for the most part correct, but then again I'm here to double check my thought processes.

Thank You in advance.

 

[TeethWhitener]

Your answers look pretty much correct. For question 1, real bonds aren't harmonic: the lengthening of bonds with energy meshes with the intuition that we can break chemical bonds by pumping enough energy into them. The reason why the anharmonic potential looks the way it does has to do with the nature of the chemical bond in question and the interactions of all the particles involved; there's no simple function that explains the shape of a chemical bond potential in general. For question 2, think about what it means to weaken the force constant (maybe graph the potential V=kx² with decreasing k and see what limit you approach--how does that compare with the analogous scenario with a particle in a box? What does this limit correspond to physically?) For question 3, I don't think there's anything to add here.

 

[pmd28]

For 1, right. I think their way of drawing that imaginary horizontal line is a little weird. But your elaboration makes perfect sense. So I have another question now regarding anharmonic oscillators: It seems that when R goes to infinity this graph will become asymptotic. Is the limit of this the energy then required to break the bond of what ever molecule we're concerned with?

For 2, I believe a weaker force constant would mean a weaker bond because the E required to move this bond would decrease. I'm not sure what I should graph V=kx² against but my intuition wants to say zero (same with PIB). But that wouldn't make sense physically because harmonic oscillators and PIB can't have zero-point energy=0. I get what the variables mean, I'm a little confused with what you're trying to coax from me.

For 3, Cool so am I right in saying "if there aren't two energetically equivalent energy levels then it's termed to have 'no degeneracy.'" ? Also that means there can never be degeneracy of 1, correct?

 

[TeethWhitener]

1. Exactly. The potential curve asymptotically approaches the bond dissociation energy.
2. Weaker force constant = weaker bond, so as k goes to zero, this is the limit of no bond/no interaction. For the particle in a box, as the box gets bigger, again, you get a limit of no interaction. Essentially, the limiting case in both instances is that of a free particle (V(x)=0 for all x), where the zero point energy is zero.
3. This is just a language thing. For many equations in statistical mechanics, you'll have to know the degeneracy of an energy level, and in this case, if the level is nondegenerate, then the degeneracy = 1. But in general, if degeneracy = 1, we typically say the energy level is nondegenerate. The two terms are synonymous

 

[pmd28]

Awesome! Thank you very much. :)