Quantum Mechanics I, finding impuls wavefunction.

[milkism]

Homework Statement

Find the impuls wavefunction phi(p) from the position wavefunction.

Relevant Equations

Look solution.

I have this following Gaussian wavefunction.

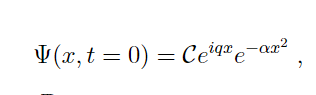
I found the constant C to be $$\sqrt{\sqrt{\frac{2 \alpha}{\pi}}}$$.
Now they're asking me to find the normalized impuls wavefunction $$\phi(p)$$. I tried to use the fourier transform relation
$$\phi (p) = \int e^{-\frac{i ( p x)}{\hbar}} \Psi (x,t=0) dx$$
and i got a long answer
$$\sqrt{\sqrt{\frac{2 \alpha}{\pi}}} \sqrt{\frac{\pi}{\alpha}} e^{-\frac{q^2}{4\alpha} + \frac{pq}{2 \alpha \hbar} - \frac{p^2}{4 \alpha \hbar ^2}}$$
Is there an other way to solve this? Because next question is to find the expectation value of position from the normalized impuls wavefunction, which is going to be very hard.

 

[milkism]

Is there a better way to find impuls wavefunctions from position wavefunctions?

 

[Orodruin]

Any other way will of course give the same result.

 

[BvU]

I found the constant C to be

How ? [edit] never mind

Because next question

Can you please post the complete problem statement ?

$\$

 

[milkism]

How ?
Can you please post the complete problem statement ?

$\$

$$\int_{-\infty}^{\infty} \Psi ^{*} \Psi dx =1, \int_{-\infty}^{\infty} C^2 e^{-2 \alpha x^2} dx = C^2 \sqrt{\frac{\pi}{2\alpha}} = 1$$

 

[milkism]

Calculate the corresponding normalized wave function φ(p) in momentum space. Explicitly compute, based on the knowledge of φ(p), the expectation value 〈x〉.

 

[BvU]

and i got a long answer

$e^{-{1\over 4\alpha}\left(q-p\right )^2}\$ doesn't look all that bad to me ...
a peak around p = q, so the exercise will probably end up at something moving to the right with momentum $q$

(did you check there is no $i$ in there ?)

The exercise reminded me of the treatment in Merzbacher, QM 2nd ed (1970 !) chapter 2.2

Next step was $$\psi(x,t) = {1\over \sqrt{2\pi}}\int_{-\infty}^{+\infty} \phi(k) e^{i(kx-\omega t}) dk$$ but I'm too rusty to comfortably work that out ( i.e. $\omega(k)$ )

$\$