SUMMARY
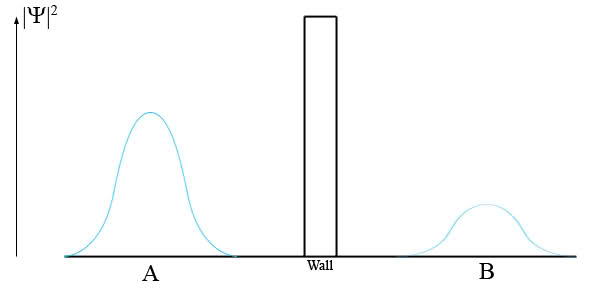
The discussion centers on quantum tunneling and its implications for energy conservation. Participants clarify that a particle can exist within a potential barrier even if its energy is lower than the barrier's potential energy (V), due to the wave-like nature of particles described by quantum mechanics. The wavefunction, denoted as psi(x,t), plays a crucial role in determining the probability of finding a particle within the barrier. The conversation also touches on the conservation of energy and momentum in quantum systems, emphasizing that these principles apply on average rather than for individual particles.
PREREQUISITES
- Understanding of quantum mechanics principles, particularly wave-particle duality.
- Familiarity with the concept of wavefunctions and their mathematical representation.
- Knowledge of potential barriers and tunneling phenomena in quantum systems.
- Basic grasp of energy conservation laws in physics.
NEXT STEPS
- Study the mathematical formulation of wavefunctions in quantum mechanics.
- Explore the implications of quantum tunneling in real-world applications, such as semiconductor physics.
- Investigate the relationship between wavefunctions and probability distributions in quantum systems.
- Learn about the conservation of energy and momentum in quantum mechanics, particularly in relation to measurements.
USEFUL FOR
Students and professionals in physics, particularly those focusing on quantum mechanics, theoretical physicists, and anyone interested in the principles of energy conservation and tunneling phenomena.