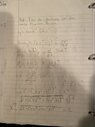Vividly
- 44
- 0
- TL;DR
- Question about inverse Tanhx
Im confused about a certain part of solving an equation. So I used the hyerbola formula to find the answer but I think I did the math wrong.
X^2-y^2=c^2
X=1
Y= (2x^5-1)^2
I did the calculations as you can see in the picture but I know I messed up on the square root part. When you square one side you have to square the whole other side.
So Far I got
1^2-((2x^5-1)^2)^2 =c^2
And as you can see in the picture the math is incorrect due to the process that's suppose to be done in math. When I square both sides I get a different answer when I simplify.
As you can see on the paper that where I am stuck because the answer is 5/2x-2x^6
X^2-y^2=c^2
X=1
Y= (2x^5-1)^2
I did the calculations as you can see in the picture but I know I messed up on the square root part. When you square one side you have to square the whole other side.
So Far I got
1^2-((2x^5-1)^2)^2 =c^2
And as you can see in the picture the math is incorrect due to the process that's suppose to be done in math. When I square both sides I get a different answer when I simplify.
As you can see on the paper that where I am stuck because the answer is 5/2x-2x^6