Master1022
- 590
- 116
- TL;DR
- This is a question about the derivation of the stream-function of a doublet using potential flow theory
Hi,
I just wanted to ask a question about the derivation of the stream function \psi for a doublet. In the pictures below is a derivation (in this one the source is on the left and the sink is on the right). I understand everything in the left photo, however my questions are:
1) Why do we divide by the distance between two sources s before taking the limit? I cannot really understand the reason provided. I understand that the sources will cancel out, but am unclear as to why that means that we need to counter that by including a \frac{1}{s} term.
2) Why does the derivation come out differently if we swap the placements of the source and sink? Intuitively, I feel that I have made an algebraic error, but I fail to see it. If we place the source on the right and the sink on the left, then we will get:
\psi = \frac{m}{2 \pi} \theta_{source} - \frac{m}{2 \pi} \theta_{sink} = \frac{m}{2 \pi} \left( atan(\frac{y}{x-s}) - atan(\frac{y}{x+s}) \right). Now we will get the same expression as before (except we have +m instead of -m), except we will end up with a different sign at the end. Surely, the end result should be the same irrespective of the original geometry.
I would appreciate any help. Thanks in advance.
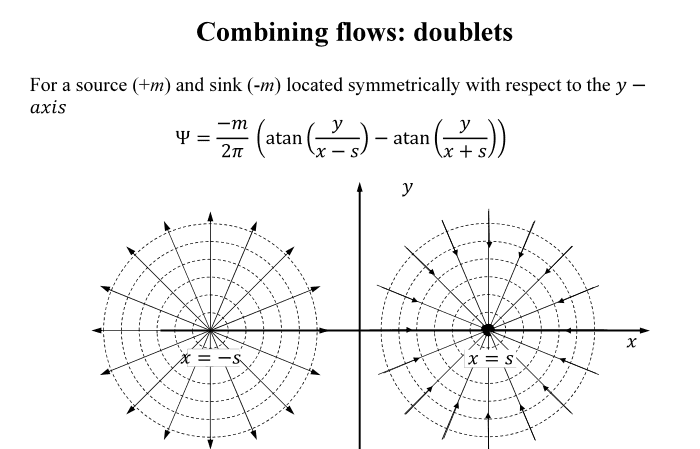
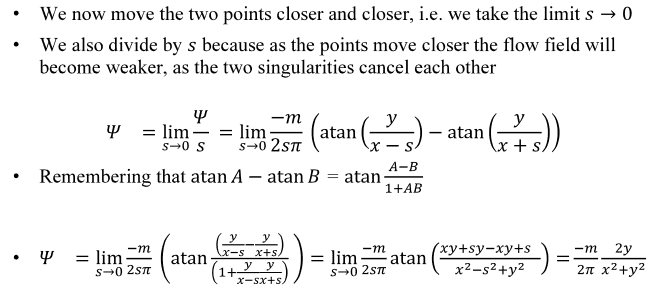
I just wanted to ask a question about the derivation of the stream function \psi for a doublet. In the pictures below is a derivation (in this one the source is on the left and the sink is on the right). I understand everything in the left photo, however my questions are:
1) Why do we divide by the distance between two sources s before taking the limit? I cannot really understand the reason provided. I understand that the sources will cancel out, but am unclear as to why that means that we need to counter that by including a \frac{1}{s} term.
2) Why does the derivation come out differently if we swap the placements of the source and sink? Intuitively, I feel that I have made an algebraic error, but I fail to see it. If we place the source on the right and the sink on the left, then we will get:
\psi = \frac{m}{2 \pi} \theta_{source} - \frac{m}{2 \pi} \theta_{sink} = \frac{m}{2 \pi} \left( atan(\frac{y}{x-s}) - atan(\frac{y}{x+s}) \right). Now we will get the same expression as before (except we have +m instead of -m), except we will end up with a different sign at the end. Surely, the end result should be the same irrespective of the original geometry.
I would appreciate any help. Thanks in advance.