Heat sink - calculating temperature at the base

[FEAnalyst]

TL;DR Summary

How to calculate a temperature at a base surface of a straight fin heat sink?

Hi,

I've checked the literature but couldn't find any formulas or examples for this particular problem involving heat sink with straight fins:

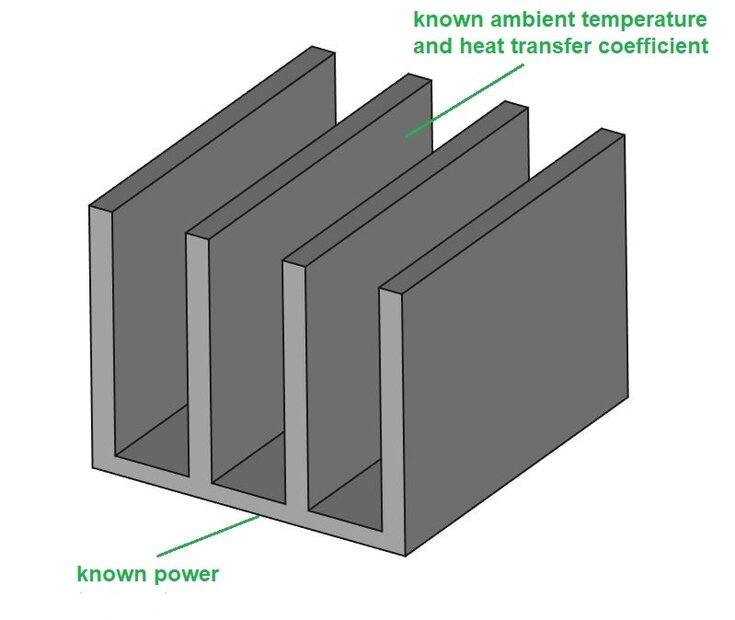
As you can see, I want to assume:
- power at the bottom surface
- convection (known ambient temperature and heat transfer coefficient) at the remaining surfaces
and calculate the temperature at the bottom surface (which should be lower than in the case when the plate has no fins).

All the formulas and examples that I've found are for different boundary conditions - know temperature or convection conditions at the bottom surface and solving for total heat flux. Here are such formulas for the case with the known temperature at the bottom surface (source: old Polish book "Heat transfer and heat exchangers" by Pudlik):
- heat dissipated from each fin: $$Q_{f}=\frac{\alpha U}{m} \cdot \left( T_{s} - T_{a} \right) \cdot tanh(mL)$$ where: $\alpha$ - heat transfer coefficient, $U$ - circumference of the fin's cross-section, $m=\sqrt{\frac{\alpha U}{\lambda A_{f}}}$, $T_{s}$ - temperature of the bottom surface, $T_{a}$ - ambient temperature, $\lambda$ - thermal conductivity, $A_{f}$ - area of the fin's cross-section.
- heat dissipated from each surface between fins: $$Q_{bf}=\alpha A \cdot \left( T_{s} - T_{a} \right)$$ where: $A$ - area of the surface between fins
- total heat flux: $$Q_{t}=n_{f} \cdot Q_{f}+n_{bf} \cdot Q_{bf}$$ where: $n_{f}$ - number of fins, $n_{bf}$ - number of surfaces between fins

This way it's possible to calculate total heat flux but how can I obtain the temperature at the bottom surface and how to replace the known temperature of the bottom surface with the known power ? Do you think that the formulas above account for all the surfaces involved in convection (all the existing surfaces apart from the bottom one) or some are omitted ?

 

[berkeman]

What is the heat sink attached to? What is generating the power that needs to be dissipated?

You probably already know this, but things like power ICs and power semiconductor devices will generally list a thermal impedance from junction-to-case in °C/Watt, so knowing the power dissipated by the junction gives you the temperature rise to the case.

https://en.wikipedia.org/wiki/Thermal_resistance

 

[FEAnalyst]

What is the heat sink attached to? What is generating the power that needs to be dissipated?

You probably already know this, but things like power ICs and power semiconductor devices will generally list a thermal impedance from junction-to-case in °C/Watt, so knowing the power dissipated by the junction gives you the temperature rise to the case.

https://en.wikipedia.org/wiki/Thermal_resistance

Thanks for the reply. Actually, I’m not doing the calculations for any particular heat sink or cooling system. It’s just an abstract problem that I want to solve with FEA first and then verify using analytical calculations. So it will be used only for educational purposes.

Do you know if it’s possible to obtain the analytical solution for these assumptions and how it could be done ?

 

[berkeman]

A part of the IC package design group that I work for now does these types of simulations for various very advanced IC packages and modules. I believe they mainly use COMSOL for the simulations, but perhaps they also use other software packages.

I think that many heat sink datasheets list their thermal resistances to air (still air or forced air), so you could probably do your simulations with the dimensions and material of a heat sink with the corresponding thermal resistance from the datasheet to compare your results.

EDIT-- Sorry, I missed that you were also asking about analytical solutions. I kind of doubt that there are any for typical heat sinks, but since the manufacturers list the thermal resistances (most likely verified with testing), that should work for checking your FEA results.

 

[FEAnalyst]

I kind of doubt that there are any for typical heat sinks

I'm also not sure if there is an analytical solution for my particular case, but, as I showed earlier, there are formulas for very similar cases only with different assumptions about the boundary conditions. It seems that thermal resistance of a heat sink can be calculated analytically as well but I'm not yet sure about the required input data.

Here's an online calculator that seems to be solving just for what I need but unfortunately they don't provide the formulas and it's even too complex since it accounts for some clearances and the result is shown for various airflow velocities while I just want to use a heat transfer coefficient:
https://myheatsinks.com/calculate/plate-fin-heat-sink-calculator/

 

[Tom.G]

I used to have a book from a major heatsink manufacturer with all that stuff spelled out. Unfortunately after several moves it seems to have entered a black hole!

HOWEVER! This site may suit your needs:
https://www.heatsinkcalculator.com/blog/sizing-heat-sinks-with-a-few-simple-equations/

(above found with:
https://www.google.com/search?&q=heat+sink+formulas)

 

[Chestermiller]

How accurate does it have to be. You know the total heat load per fin and you know the base area per fin.

 

[FEAnalyst]

I used to have a book from a major heatsink manufacturer with all that stuff spelled out. Unfortunately after several moves it seems to have entered a black hole!

HOWEVER! This site may suit your needs:
https://www.heatsinkcalculator.com/blog/sizing-heat-sinks-with-a-few-simple-equations/

By any chance, do you remember the name of this manufacturer ? Maybe I will be able to get this book.

I checked this site and it's really interesting but unfortunately covers only radiation and natural convection while I need a different set of formulas.

How accurate does it have to be. You know the total heat load per fin and you know the base area per fin.

My goal is to compare the numerical solution with the analytical one so accuracy is pretty important but the approximate approach will be a good start. I've been looking everywhere but couldn't find any formulas and examples for the case with known power at the bottom surface and unknown temperature at this location.

 

[Chestermiller]

By any chance, do you remember the name of this manufacturer ? Maybe I will be able to get this book.

I checked this site and it's really interesting but unfortunately covers only radiation and natural convection while I need a different set of formulas.My goal is to compare the numerical solution with the analytical one so accuracy is pretty important but the approximate approach will be a good start. I've been looking everywhere but couldn't find any formulas and examples for the case with known power at the bottom surface and unknown temperature at this location.

You are aware that, if the flux is uniform at the base, then the temperature is not, and, if the temperature is uniform at the base, then the flux is not, right?

A first approximation to the average flux at the base is the total heat load (based on your solution for a constant temperature at the base of the fin) divided by the base area per fin.

Draw yourself a picture of what you think the heat flow lines look like and what you think the isotherms look like.

 

[FEAnalyst]

You are aware that, if the flux is uniform at the base, then the temperature is not, and, if the temperature is uniform at the base, then the flux is not, right?

A first approximation to the average flux at the base is the total heat load (based on your solution for a constant temperature at the base of the fin) divided by the base area per fin.

Draw yourself a picture of what you think the heat flow lines look like and what you think the isotherms look like.

I can see the distribution of temperature and heat flux in my case thanks to the numerical solution. I’ve noticed that it’s not uniform but I will be fine with just the maximum value.

The calculator that I linked in one of the previous posts seems to be solving just for what I need (or even more than I need). So it should be possible to do it analytically somehow. Unfortunately, they didn’t provide the formulas and I’m trying to find them somewhere else.

 

[Chestermiller]

Are you saying that you are unaware of how to set up the analytic solution for a cooling fin? I can show you how to do this analysis, and also the corresponding analysis for the base, if the scale on your figure is approximately correct. Do you want me to set up the fin part of the derivation for you? The part for the base is going to be somewhat similar. You just need to get them to match.

 

[FEAnalyst]

Are you saying that you are unaware of how to set up the analytic solution for a cooling fin? I can show you how to do this analysis, and also the corresponding analysis for the base, if the scale on your figure is approximately correct. Do you want me to set up the fin part of the derivation for you? The part for the base is going to be somewhat similar. You just need to get them to match.

I have some analytical solutions (formulas in my first post) for heat flux in each fin and surface between fins. The problem is that I don’t know how to use these (or other) equations in my case where power at the bottom surface is given and temperature of that surface has to be calculated.

The picture attached to my initial post is a screenshot of the 3D model used for simulation so proportions are correct. Of course I can also provide the dimensions.

I rarely deal with heat transfer problems (most of my analyses involve solid mechanics) and this domain is still somewhat unintuitive for me.

 

[Chestermiller]

The 1D model of a cooling fin goes like this. Let w be the width of the fin, D be the depth of the fin, and y be the vertical coordinate along the fin. A heat balance on the portion of the fin between y and $y+\Delta y$ goes like this: $$[q(y)-q(y+\Delta y)]wD=2UD\Delta y(T-T_0)$$where q is the vertical heat flux ($q=-k\frac{dT}{dy}$), U is the heat transfer coefficient, T(y) is the temperature at y, and $T_0$ is the outside temperature. Taking the limit as $\Delta y$ goes to zero gives: $$kw\frac{d^2T}{dy^2}-2U(T-T_0)=0$$

OK so far?

 

[FEAnalyst]

The 1D model of a cooling fin goes like this. Let w be the width of the fin, D be the depth of the fin, and y be the vertical coordinate along the fin. A heat balance on the portion of the fin between y and $y+\Delta y$ goes like this: $$[q(y)-q(y+\Delta y)]wD=2UD\Delta y(T-T_0)$$where q is the vertical heat flux ($q=-k\frac{dT}{dy}$), U is the heat transfer coefficient, T(y) is the temperature at y, and $T_0$ is the outside temperature. Taking the limit as $\Delta y$ goes to zero gives: $$kw\frac{d^2T}{dy^2}-2U(T-T_0)=0$$

OK so far?

Yes, that's similar to the derivation in my books. Later on, they arrive at the $m$ coefficient and final formula for heat flux from the fin. But the temperature at the bottom surface must be known here.

 

[Chestermiller]

Yes, that's similar to the derivation in my books. Later on, they arrive at the $#m$# coefficient and final formula for heat flux from the fin. But the temperature at the bottom surface must be known here.

Are you saying you are comfortable with this equation and that it is OK to continue?
Please have faith. I'll get you to the final approximate analytical result you are looking for (for comparison with your FEM calculations). But it will involve your participation.

 

[FEAnalyst]

Are you saying you are comfortable with this equation and that it is OK to continue?
Please have faith. I'll get you to the final approximate analytical result you are looking for (for comparison with your FEM calculations). But it will involve your participation.

Yes, please continue. My math is a bit rusty but I like to refresh my knowledge and so far the derivation is clear.

 

[Chestermiller]

Going back to your original post, there is a way of approximating what you want. You are assuming that the heat flux at the base is uniform, and you want to find the temperature variation at the base. For the approximation in your original post, there are going to be two temperature regions: (1) directly under the fin and (2) in the region between the fins. These are described by the two equations you presented in your original post. The only difference is going to be that, for your second equation, you are going to be using a different temperature than Ts. This is going to be chosen so that the heat flux in the region between the fins is equal to the vertical heat flux at the base of each fin. It's as simple as that.

 

[FEAnalyst]

Going back to your original post, there is a way of approximating what you want. You are assuming that the heat flux at the base is uniform, and you want to find the temperature variation at the base. For the approximation in your original post, there are going to be two temperature regions: (1) directly under the fin and (2) in the region between the fins. These are described by the two equations you presented in your original post. The only difference is going to be that, for your second equation, you are going to be using a different temperature than Ts. This is going to be chosen so that the heat flux in the region between the fins is equal to the vertical heat flux at the base of each fin. It's as simple as that.

This approach makes sense but I'm not sure how to modify the equations. The first one (heat dissipated from each fin) should remain unchanged and only the second one (heat dissipated from each surface between fins) should be modified ? They both describe total heat flux and don't include any parameter describing the coordinate along the fin (like $y$).

 

[Chestermiller]

This approach makes sense but I'm not sure how to modify the equations. The first one (heat dissipated from each fin) should remain unchanged and only the second one (heat dissipated from each surface between fins) should be modified ? They both describe total heat flux and don't include any parameter describing the coordinate along the fin (like $y$).

The y has been integrated out. The heat flux at the base of the fin is the total heat dissipated divided by the cross sectional area of the fin. The heat flux in the region between the fins is the heat dissipated between fins divided by the cross sectional area of the base. In your calculation, both heat fluxes are equal.

 

[FEAnalyst]

The y has been integrated out. The heat flux at the base of the fin is the total heat dissipated divided by the cross sectional area of the fin. The heat flux in the region between the fins is the heat dissipated between fins divided by the cross sectional area of the base. In your calculation, both heat fluxes are equal.

So it should go like this: $$q_{f-base}=q_{bf}$$ $$\frac{Q_{f}}{A_{f}}=\frac{Q_{bf}}{A}$$ right ?

Now I should solve for $T_{s}$ in the $Q_{bf}$ equation (since that's what I'm looking for). But the first formula (for $Q_{f}$) also includes this parameter. And I need to substitute the power at the base somewhere. Should it go directly as $Q_{bf}$ or am I misinterpreting something ?

 

[Chestermiller]

So it should go like this: $$q_{f-base}=q_{bf}$$ $$\frac{Q_{f}}{A_{f}}=\frac{Q_{bf}}{A}$$ right ?

Now I should solve for $T_{s}$ in the $Q_{bf}$ equation (since that's what I'm looking for). But the first formula (for $Q_{f}$) also includes this parameter. And I need to substitute the power at the base somewhere. Should it go directly as $Q_{bf}$ or am I misinterpreting something ?

The Ts in the Qbf equation is a different value from the Ts in the Qf equation. Call it Ts'. That's what you solve for.

 

[FEAnalyst]

The Ts in the Qbf equation is a different value from the Ts in the Qf equation. Call it Ts'. That's what you solve for.

$$\frac{\frac{\alpha U}{m} \cdot \left( T_{s} - T_{a} \right) \cdot tanh \left( \sqrt{\frac{\alpha U}{\lambda A_{f}}} L \right)}{A_{f}}=\frac{\alpha A \cdot \left( T_{s}^{\prime}-T_{a} \right)}{A}$$
Is it correct ? Now I should solve for $T_{s}^{\prime}$ but I don't know $T_{s}$ - temperature at the base of each fin. And I still have to substitute that power applied to the bottom surface somewhere in the equation.

 

[Chestermiller]

$$\frac{\frac{\alpha U}{m} \cdot \left( T_{s} - T_{a} \right) \cdot tanh \left( \sqrt{\frac{\alpha U}{\lambda A_{f}}} L \right)}{A_{f}}=\frac{\alpha A \cdot \left( T_{s}^{\prime}-T_{a} \right)}{A}$$
Is it correct ? Now I should solve for $T_{s}^{\prime}$ but I don't know $T_{s}$ - temperature at the base of each fin. And I still have to substitute that power applied to the bottom surface somewhere in the equation.

First you specify a value for Ts-To. Then you calculate Qf/Af. This is the uniform heat flux over the entire base that you are imposing. Then you calculate Ts'-To. This is the temperature in the web between the fins. These three quantities are all proportional to one another. So you can change the value of Ts-To until you get the uniform heat flux you actually want.

 

[FEAnalyst]

First you specify a value for Ts-To. Then you calculate Qf/Af. This is the uniform heat flux over the entire base that you are imposing. Then you calculate Ts'-To. This is the temperature in the web between the fins. These three quantities are all proportional to one another. So you can change the value of Ts-To until you get the uniform heat flux you actually want.

Let's say that I want to apply a power of $80 \ W$ to the base of the heat sink and find the base temperature. Then I should:
1) make an initial guess for $T_{s}$
2) calculate $\frac{Q_{f}}{A_{f}}$
3) find $T_{s}^{\prime}$
4) repeat until total heat flux $Q_{t}=80 \ W$
Is that right ?

 

[Chestermiller]

Let's say that I want to apply a power of $80 \ W$ to the base of the heat sink and find the base temperature. Then I should:
1) make an initial guess for $T_{s}$
2) calculate $\frac{Q_{f}}{A_{f}}$
3) find $T_{s}^{\prime}$
4) repeat until total heat flux $Q_{t}=80 \ W$
Is that right ?

yes, but Qt is going to be proportional to Ts-To. So you don't need to iterate.

 

[FEAnalyst]

yes, but Qt is going to be proportional to Ts-To. So you don't need to iterate.

Below are my calculations. I must be doing something wrong because the result is around $1655^{\circ} C$. The values should be correct since I use a computer algebra system and likely the problem lies in the calculation method. Could you take a look ?

Input data: $\alpha=15 \ \frac{W}{m^{2}K}$, $\lambda=237 \ \frac{W}{mK}$, $T_{a}=20^{\circ} C$, $A=768 \ mm^{2}$, $A_{f}=240 \ mm^{2}$, $U=128 \ mm$, $L=40 \ mm$, $n_{f}=4$, $n_{bf}=3$

I assume that the power at the bottom surface is $80 \ W$. I obtain the total heat flux $Q_{t}=80 \ W$ for $T_{s}=98^{\circ} C$. But here's what I get as $T_{s}^{\prime}$ in this case: $$m=\sqrt{\frac{\alpha U}{\lambda A_{f}}}=\sqrt{\frac{15 \cdot 0.128}{237 \cdot 0.00024}}=5.809929 \ \frac{1}{m}$$ $$Q_{f}=\frac{\alpha U}{m} \cdot \left( T_{s} - T_{a} \right) \cdot tanh(mL)=\frac{15 \cdot 0.128}{m} \cdot \left( 98 - 20 \right) \cdot tanh(5.809929 \cdot 0.04)=5.884836 \ W$$ $$q_{f-base}=\frac{Q_{f}}{A_{f}}=\frac{5.884836}{0.00024}=24520.149604 \ \frac{W}{m^{2}}$$ $$\frac{\alpha A \left( T_{s}^{\prime} - T_{a} \right)}{A}=q_{f-base}$$ $$\frac{15 \cdot 0.000768 \cdot \left( T_{s}^{\prime} - 20 \right)}{0.000768}=24520.149604$$ $$T_{s}^{\prime}=1654.67664^{\circ} C$$ $$Q_{bf}=\alpha A \left( T_{s}^{\prime} - T_{a} \right)=15 \cdot 0.000768 \cdot \left( 1654.67664-20 \right)=18.831475 \ W$$ $$Q_{t}=n_{f} \cdot Q_{f} + n_{bf} \cdot Q_{bf}=80.033768 \ W$$

 

[Chestermiller]

Suppose there were no fins, just a flat slab. What would the temperature have to be to produce a heat flow of 80 W?

You have fins that are 2 mm x 62 mm, right? And spaces between the fins of about 12.5 mm, right? How many fins and how many spaces between them are there? What is the total base area of the assembly?

 

[FEAnalyst]

Suppose there were no fins, just a flat slab. What would the temperature have to be to produce a heat flow of 80 W?

The formula for a flat plate is $Q=\alpha A \left( T_{s}-T_{a} \right)$ so the temperature would have to be $1654^{\circ} C$. I may have exaggerated a bit with the assumed power. But still, the result doesn't make sense because I got the same value for the plate with fins. I must be doing something wrong in this calculation.

You have fins that are 2 mm x 62 mm, right? And spaces between the fins of about 12.5 mm, right? How many fins and how many spaces between them are there? What is the total base area of the assembly?

Here are the dimensions:
- fin's width: $4 \ mm$
- fin's depth: $60 \ mm$
- fin's height: $40 \ mm$
- distance between the fins: $12.8 \ mm$
- base surface area: $54.4 \cdot 60=3264 \ mm^{2}$

 

[Chestermiller]

The formula for a flat plate is $Q=\alpha A \left( T_{s}-T_{a} \right)$ so the temperature would have to be $1654^{\circ} C$. I may have exaggerated a bit with the assumed power. But still, the result doesn't make sense because I got the same value for the plate with fins. I must be doing something wrong in this calculation.Here are the dimensions:
- fin's width: $4 \ mm$
- fin's depth: $60 \ mm$
- fin's height: $40 \ mm$
- distance between the fins: $12.8 \ mm$
- base surface area: $54.4 \cdot 60=3264 \ mm^{2}$

View attachment 296284

What these results are telling us is that most of the entering heat leaves through the fins, and most of the heat that enters through the web between the fins flows horizontally to the fins. Only a small fraction is flowing into the air above the web. This means that the web is going to be approximately the same temperature as the base of the fins, and that your original equations in post #1 are going to be the correct ones to use, with Ts=Ts'. So try the problem again using these equations and see what you get. The heat load at the base is going to be equal to the sum of the two heats from the two equations.

 

[Tom.G]

Uhmm... Something doesn't match here.

You have fins that are 2 mm x 62 mm, right?

- fin's width: 4 mm
- fin's depth: 60 mm
- fin's height: 40mm

 

[Chestermiller]

Uhmm... Something doesn't match here.

Oops. My mistake.

 

[FEAnalyst]

What these results are telling us is that most of the entering heat leaves through the fins, and most of the heat that enters through the web between the fins flows horizontally to the fins. Only a small fraction is flowing into the air above the web. This means that the web is going to be approximately the same temperature as the base of the fins, and that your original equations in post #1 are going to be the correct ones to use, with Ts=Ts'. So try the problem again using these equations and see what you get. The heat load at the base is going to be equal to the sum of the two heats from the two equations.

Thank you very much, now the result makes much more sense. I got $Q_{t}=80 \ W$ for $T_{s}=258^{\circ}C$ while the value from simulation (maximum temperature at the base) is $244^{\circ}C$ when $80 \ W$ are applied to the base. Here are my calculations: $$Q_{f}=\frac{\alpha U}{\sqrt{\frac{\alpha U}{\lambda A_{f}}}} \cdot \left( T_{s} - T_{a} \right) \cdot tanh \left( \sqrt{\frac{\alpha U}{\lambda A_{f}}} L \right)$$ $$Q_{f}=\frac{15 \cdot 0.128}{\sqrt{\frac{15 \cdot 0.128}{237 \cdot 0.00024}}} \cdot \left( 258 - 20 \right) \cdot tanh \left( \sqrt{\frac{15 \cdot 0.128}{237 \cdot 0.00024}} 0.04 \right)=17.9563 \ W$$ $$Q_{bf}=\alpha A \cdot \left( T_{s} - T_{a} \right)=15 \cdot 0.000768 \cdot \left( 258 - 20 \right)=2.7418 \ W$$ $$Q_{t}=n_{f} \cdot Q_{f} + n_{bf} \cdot Q_{bf}=4 \cdot 17.9563 + 3 \cdot 2.7418=80.0505 \ W$$ I wonder if there is a way to increse the accuracy of these hand calculations. The approach used here is approximate but maybe there's no better analytical method.

 

[berkeman]

Thanks for the reply. Actually, I’m not doing the calculations for any particular heat sink or cooling system. It’s just an abstract problem that I want to solve with FEA first and then verify using analytical calculations. So it will be used only for educational purposes.

-------------------------------------------------------

-------------------------------------------------------

Sorry, I just dropped into the thread to see how it's going, and I see that Chet is giving you great help. But I do need to take issue with those 244-258°C numbers. That is way too high for any real semiconductor device or transformer device. I know that this is just a numerical exercise, but a good extension would be to figure out how big the heatsink needs to be for a practical semiconductor product. Also what difference it makes to turn the heatsink to the vertical orientation, and what difference it makes to use forced air flowing across the heatsink.
https://www.analog.com/media/en/training-seminars/tutorials/mt-093.pdf

 

[gmax137]

If I may interject here, this thread brings to mind a quote from President James A. Garfield: “The ideal college is Mark Hopkins on one end of a log and a student on the other.”

You can look up those people if you want but the point is, a dedicated talented teacher interacting one on one with a dedicated willing student. Awesome to see in practice. PF can be a joy.

Kudos to @Chestermiller and @FEAnalyst

 

[Tom.G]

@FEAnalyst
Since you seem to have found your solution this is a bit dated, but for completeness, here goes anyhow.

Way back in post #6 I mentioned a book about heat sinks, and you responded:

By any chance, do you remember the name of this manufacturer ? Maybe I will be able to get this book.

I checked this site and it's really interesting but unfortunately covers only radiation and natural convection while I need a different set of formulas.

I stumbled across this thread today, re-searched for the book, and found it!

Title: HEAT SINK APPLICATION HANDBOOK
Publisher: AHAM

968 W. Foothill Blvd., Azusa California, 91702, ph (213) 334-5135​

2 Gill St. Bldg. 5, Woburn, Massachusetts, 01801, ph (617) 935-4350​

Pages: 180
Publication Date: 1974
5¼ x 7¾ inches, perfect-bound paper back, cover price USD $9.50

A Google search (https://www.google.com/search?&q=aham+heatsink) shows it is now "AHAM Tor Inc."

A semiconductor AP Note from 1993 shows:
AHAM-TOR Heatsinks, 27901 Front St, Rancho, California, 92390, (714) 676-4151

A quick and cursory look thru the book indicates that although it addresses Fin Shape, Conductivity, etc., it mostly concerns the interface calculations rather than the heat flow details within the heatsink itself.

Cheers,
Tom