- #1
sankalpmittal
- 785
- 15
Question--- Angular Simple Harmonic motion..
A spherical ball of mass "m" and radius "r" rolls without slipping on a rough concave surface of large radius "R". It makes small oscillations about the lowest point. Find the time period of such oscillations.
http://en.wikipedia.org/wiki/Simple_harmonic_motion
http://postimg.org/image/whgt6dvvb/
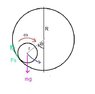
In the last line of the image above, the formula, Time period = 2π√(I/Mgl)
Where "l" is the distance between the point of suspension and centre of mass of physical pendulum. Why does this formula fail in this case ?
It yields :
l= R-r
I= 2mr2/5 + m(R-r)2
On putting these values in formula, Time period = 2π√(I/Mgl), why I keep getting the wrong answer ?
Please helps !
Thanks in advance...
Homework Statement
A spherical ball of mass "m" and radius "r" rolls without slipping on a rough concave surface of large radius "R". It makes small oscillations about the lowest point. Find the time period of such oscillations.
Homework Equations
http://en.wikipedia.org/wiki/Simple_harmonic_motion
The Attempt at a Solution
http://postimg.org/image/whgt6dvvb/
In the last line of the image above, the formula, Time period = 2π√(I/Mgl)
Where "l" is the distance between the point of suspension and centre of mass of physical pendulum. Why does this formula fail in this case ?
It yields :
l= R-r
I= 2mr2/5 + m(R-r)2
On putting these values in formula, Time period = 2π√(I/Mgl), why I keep getting the wrong answer ?
Please helps !
Thanks in advance...
Last edited by a moderator: