Question from Jesse about Gaussian Elimination and LU factorisation.

[Prove It]

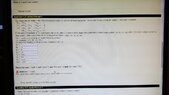
View attachment 5370

This system can be written as a matrix equation $\displaystyle \begin{align*} A\,\mathbf{x} = \mathbf{b} \end{align*}$ as

$\displaystyle \begin{align*} \left[ \begin{matrix} \phantom{-}2 & 4 & \phantom{-}0 & 1 \\ \phantom{-}2 & 8 & -2 & 7 \\ -2 & 2 & -2 & 7 \\ \phantom{-}0 & 8 & -5 & 11 \end{matrix} \right] \left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{matrix} \right] = \left[ \begin{matrix} \phantom{-}7 \\ \phantom{-}3 \\ -7 \\ -12 \end{matrix} \right] \end{align*}$

To get the LU factorisation we need to use Gaussian Elimination on the coefficient matrix...

$\displaystyle \begin{align*} A = \left[ \begin{matrix} \phantom{-}2 & 4 & \phantom{-}0 & 1 \\ \phantom{-}2 & 8 & -2 & 7 \\ -2 & 2 & -2 & 7 \\ \phantom{-}0 & 8 & -5 & 11 \end{matrix} \right] \end{align*}$

To eliminate the terms under the main diagonal in the first column, we will apply Row 2 - Row 1 to Row 3 and Row 3 - (-1)Row 1 to Row 3. As we are eliminating the elements $\displaystyle \begin{align*} a_{2,1} \end{align*}$ and $\displaystyle \begin{align*} a_{3, 1} \end{align*}$, that means in our lower triangular matrix, which has 1 as all the elements on the main diagonal and the multipliers of the rows as its coefficients under the main diagonal, will have $\displaystyle \begin{align*} \mathcal{l}_{2,1} = 1 \end{align*}$ and $\displaystyle \begin{align*} \mathcal{l}_{3,1} = -1 \end{align*}$. Since we didn't have to do anything with element $\displaystyle \begin{align*} a_{4,1} \end{align*}$ that means the multiplier is 0, and thus $\displaystyle \begin{align*} \mathcal{l}_{4,1} = 0 \end{align*}$. A has now become

$\displaystyle \begin{align*} \left[ \begin{matrix} 2 & 4 & \phantom{-}0 & 1 \\ 0 & 4 & -2 & 6 \\ 0 & 6 & -2 & 8 \\ 0 & 8 & -5 & 11 \end{matrix} \right] \end{align*}$

To eliminate the terms under the main diagonal in the second column, we will apply Row 3 - (3/2)Row 2 to Row 3 and Row 4 - 2 Row 2 to Row 4. As we are eliminating the elements $\displaystyle \begin{align*} a_{3,2} \end{align*}$ and $\displaystyle \begin{align*} a_{4,2} \end{align*}$, this means that $\displaystyle \begin{align*} \mathcal{l}_{3,2} = \frac{3}{2} \end{align*}$ and $\displaystyle \begin{align*} \mathcal{l}_{4,2} = 2 \end{align*}$. A has now become

$\displaystyle \begin{align*} \left[ \begin{matrix} 2 & 4 & \phantom{-}0 & \phantom{-}1 \\ 0 & 4 & -2 & \phantom{-}6 \\ 0 & 0 & \phantom{-}1 & -1 \\ 0 & 0 & -1 & \phantom{-}1 \end{matrix} \right] \end{align*}$

To eliminate the term under the main diagonal in the third column, we will apply Row 4 - (-1)Row 3 to Row 4. As we are eliminating the element $\displaystyle \begin{align*} a_{4,3} \end{align*}$ that means that $\displaystyle \begin{align*} \mathcal{l}_{4,3} = -1 \end{align*}$. A has now become

$\displaystyle \begin{align*} \left[ \begin{matrix} 2 & 4 & \phantom{-}0 & \phantom{-}1 \\ 0 & 4 & -2 & \phantom{-}6 \\ 0 & 0 & \phantom{-}1 & -1 \\ 0 & 0 & \phantom{-}0 & -2 \end{matrix} \right] \end{align*}$

So we have found that our lower triangular matrix $\displaystyle \begin{align*} L = \left[ \begin{matrix} \phantom{-}1 & 0 & \phantom{-}0 & 0 \\ \phantom{-}1 & 1 & \phantom{-}0 & 0 \\ -1 & \frac{3}{2} & \phantom{-}1 & 0 \\ \phantom{-}0 & 2 & -1 & 1 \end{matrix} \right] \end{align*}$ and our upper triangular matrix $\displaystyle \begin{align*} U = \left[ \begin{matrix} 2 & 4 & \phantom{-}0 & \phantom{-}1 \\ 0 & 4 & -2 & \phantom{-}6 \\ 0 & 0 & \phantom{-}1 & -1 \\ 0 & 0 & \phantom{-}0 & -2 \end{matrix} \right] \end{align*}$.

This reduces the system to $\displaystyle \begin{align*} L\,U\,\mathbf{x} = \mathbf{b} \end{align*}$. Notice that $\displaystyle \begin{align*} U\,\mathbf{x} \end{align*}$ is a column matrix when multiplied out, which we can call $\displaystyle \begin{align*} \mathbf{g} \end{align*}$. This now reduces the system to two simpler matrix equations, as the coefficient matrices are diagonal. They are $\displaystyle \begin{align*} L\,\mathbf{g} = \mathbf{b} \end{align*}$ and $\displaystyle \begin{align*} U\,\mathbf{x} = \mathbf{g} \end{align*}$.

Solving for $\displaystyle \begin{align*} \mathbf{g} \end{align*}$ we have

$\displaystyle \begin{align*} \left[ \begin{matrix} \phantom{-}1 & 0 & \phantom{-}0 & 0 \\ \phantom{-}1 & 1 & \phantom{-}0 & 0 \\ -1 & \frac{3}{2} & \phantom{-}1 & 0 \\ \phantom{-}0 & 2 & -1 & 1 \end{matrix} \right] \left[ \begin{matrix} g_1 \\ g_2 \\ g_3 \\ g_4 \end{matrix} \right] = \left[ \begin{matrix} \phantom{-}7 \\ \phantom{-}3 \\ -7 \\ -12 \end{matrix} \right] \end{align*}$

We can see $\displaystyle \begin{align*} g_1 = 7 \end{align*}$. Forward substituting gives

$\displaystyle \begin{align*} g_1 + g_2 &= 3 \\ 7 + g_2 &= 3 \\ g_2 &= -4 \end{align*}$

Forward substituting gives

$\displaystyle \begin{align*} -g_1 + \frac{3}{2}\,g_2 + g_3 &= -7 \\ -7 - 6 + g_3 &= -7 \\ g_3 &= 6 \end{align*}$

Forward substituting gives

$\displaystyle \begin{align*} 2\,g_2 - g_3 + g_4 &= -12 \\ -8 - 6 + g_4 &= -12 \\ -14 + g_4 &= -12 \\ g_4 &= 2 \end{align*}$

Now solving $\displaystyle \begin{align*} U\,\mathbf{x} = \mathbf{g} \end{align*}$ for $\displaystyle \begin{align*} \mathbf{x} \end{align*}$ gives

$\displaystyle \begin{align*} \left[ \begin{matrix} 2 & 4 & \phantom{-}0 & \phantom{-}1 \\ 0 & 4 & -2 & \phantom{-}6 \\ 0 & 0 & \phantom{-}1 & -1 \\ 0 & 0 & \phantom{-}0 & -2 \end{matrix} \right] \left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{matrix} \right] = \left[ \begin{matrix} \phantom{-}7 \\ -4 \\ \phantom{-}6 \\ \phantom{-}2 \end{matrix} \right] \end{align*}$

We can see that

$\displaystyle \begin{align*} -2x_4 &= 2 \\ x_4 &= -1 \end{align*}$

Back substituting gives

$\displaystyle \begin{align*} x_3 - x_4 &= 6 \\ x_3 + 1 &= 6 \\ x_3 &= 5 \end{align*}$

Back substituting gives

$\displaystyle \begin{align*} 4\,x_2 - 2\,x_3 + 6\,x_4 &= -4 \\ 4\,x_2 - 10 - 6 &= -4 \\ 4\,x_2 &= 12 \\ x_2 &= 3 \end{align*}$

Back substituting gives

$\displaystyle \begin{align*} 2\,x_1 + 4\,x_2 + x_4 &= 7 \\ 2\,x_1 + 12 - 1 &= 7 \\ 2\,x_1 &= -4 \\ x_1 &= -2 \end{align*}$

So to answer your question we have $\displaystyle \begin{align*} g_1 = 7 , \, g_2 = -4 , \, g_3 = 6 , \, g_4 = 2, \, x_1 = -2 , \, x_2 = 3 , \, x_3 = 5 \end{align*}$ and $\displaystyle \begin{align*} x_4 = -1 \end{align*}$.

 

[member38644]

Thank you for the detailed explanation, it was very helpful! It's interesting to see how the Gaussian Elimination process can be broken down into smaller, simpler equations.