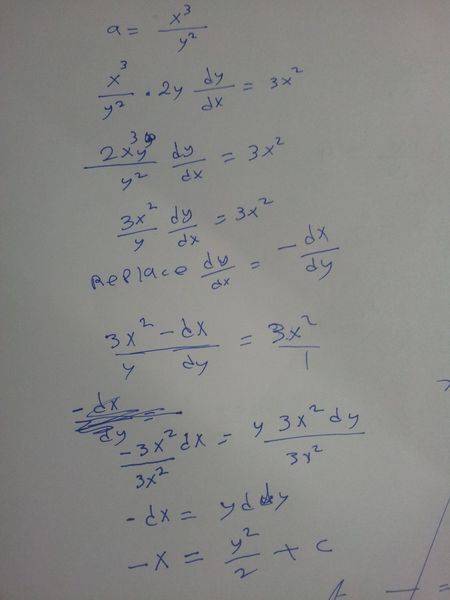Question in orthogonal trajectories

Thread starter manal950
Start date Feb 23, 2013
Tags

Orthogonal Trajectories

Click For Summary

SUMMARY

The discussion centers on the calculation of orthogonal trajectories for the family of curves defined by the equation g(x, y) = x³/y² = a. The user presents the differential equation 2ay/dx = 3x² and seeks validation of their answer. The correct approach involves calculating the gradients ∇f and ∇g, where ∇g = (3x²/y², -2x³/y³) and ∇f = (1, 2y). The condition for orthogonality is established by ensuring that ∇f.∇g = 0, leading to the equation 3x²/y² - 4x³/y² = 0.

PREREQUISITES

Understanding of differential equations and their applications.
Familiarity with the concept of orthogonal trajectories in calculus.
Knowledge of gradient vectors and their significance in multivariable calculus.
Proficiency in manipulating algebraic expressions involving polynomials.

NEXT STEPS

Study the method for finding orthogonal trajectories in detail.
Learn about gradient vectors and their applications in optimization problems.
Explore the implications of the condition ∇f.∇g = 0 in multivariable calculus.
Practice solving differential equations related to families of curves.

USEFUL FOR

Students and professionals in mathematics, particularly those studying calculus and differential equations, as well as educators looking to enhance their understanding of orthogonal trajectories.

Feb 23, 2013

manal950

answer b

I forget first step

2aydy/dx = 3x^2

please can check my answer

Physics news on Phys.org

Feb 23, 2013

haruspex

Science Advisor

Homework Helper

Insights Author

Gold Member

2024 Award

I'm not able to follow the logic of your method, but it does not seem to give a valid answer. The original family is g(x, y) = x³/y² = a; if your answer f(x, y) = y²+x = c is correct then you should find ∇f.∇g = 0. ∇g = (3x²/y², -2x³/y³); ∇f = (1, 2y); ∇f.∇g = 3x²/y² - 4x³/y².

Thread 'Distance between a Clock's hands when the distance is increasing most rapidly'

Question: A clock's minute hand has length 4 and its hour hand has length 3. What is the distance between the tips at the moment when it is increasing most rapidly?(Putnam Exam Question) Answer: Making assumption that both the hands moves at constant angular velocities, the answer is ## \sqrt{7} .## But don't you think this assumption is somewhat doubtful and wrong?

View full post »