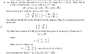Sciencer
- 8
- 0
Hi guys,
I am taking this class in lie groups but the professor never introduced the concept of quaternion and he asked about it. I saw from google the properties of multiplications of j and I made the multiplication according to
(B + jC)(u + jv) = Bu + Bjv + jCu + j^2Cv = Bu - Cv + j(Cu + Bv)
but in his answer its C^* and B^* so I was wondering how did he come up with that?
I am taking this class in lie groups but the professor never introduced the concept of quaternion and he asked about it. I saw from google the properties of multiplications of j and I made the multiplication according to
(B + jC)(u + jv) = Bu + Bjv + jCu + j^2Cv = Bu - Cv + j(Cu + Bv)
but in his answer its C^* and B^* so I was wondering how did he come up with that?