himynameJEF
- 5
- 0
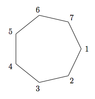
Let G be the group of symmetries (including flips) of the regular heptagon (7-gon).
View attachment 8446
As usual, we regard the elements of G as permutations of the set of vertex labels; thus, G ≤ S7.
(a) Let σ denote the rotation of the 7-gon that takes the vertex 1 to the vertex 2. Write down the cyclic subgroup R := ⟨σ⟩ as a set of elements of S7 in cycle notation.
(b) What are the orders of each of the elements of R?
does this mean R := ⟨( 1 2 3 4 5 6 7 )⟩?
and I am unsure how to answer part b)
thanks
View attachment 8446
As usual, we regard the elements of G as permutations of the set of vertex labels; thus, G ≤ S7.
(a) Let σ denote the rotation of the 7-gon that takes the vertex 1 to the vertex 2. Write down the cyclic subgroup R := ⟨σ⟩ as a set of elements of S7 in cycle notation.
(b) What are the orders of each of the elements of R?
does this mean R := ⟨( 1 2 3 4 5 6 7 )⟩?
and I am unsure how to answer part b)
thanks