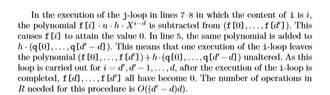Questions about analysis of algorithm

[evinda]

Hello! (Wave)

The following algorithm is given:

View attachment 7522

And it says the following:

View attachment 7523

First of all, at the first line do they mean that the content of j is i?

About the second line, why don't we subtract the polynomial $f \cdot u \cdot h \cdot X^i $ from $(f[0], \dots, f[d'])$?

Is there then maybe an error at the algorithm at the line 8? Because at the first iteration for i=d' and j=i=d' we would get f[d']<-f[d']-uf[d']h[d'], but h[d'] is 0, when we suppose that d<d'. So should it maybe be f[j]<-f[j]-ah[j-d] ?Also, what do they mean at the part <<In line 5... unaltered.>> ? At line 5 of the algorithm, we have a<-u*f. Why is it said that the polynomial $f \cdot u \cdot h \cdot X^{i-d}$ is added to $h \cdot (q[0], \dots, q[d'-d])$ ? (Thinking)

 

[I like Serena]

First of all, at the first line do they mean that the content of j is i?

Hi evinda! (Smile)

Yep. I think so too.

About the second line, why don't we subtract the polynomial $f \cdot u \cdot h \cdot X^i $ from $(f[0], \dots, f[d'])$?

Wouldn't we multiply $(f_{d'}\cdot u \cdot X^{d'-d})$ with $(h_dX^d+h_{d-1}X^{d-1} +... + h_0)$ to get $(f_{d'}X^{d'}+...)$? (Wondering)
So I think it is correct as it is given.

Is there then maybe an error at the algorithm at the line 8? Because at the first iteration for i=d' and j=i=d' we would get f[d']<-f[d']-uf[d']h[d'], but h[d'] is 0, when we suppose that d<d'. So should it maybe be f[j]<-f[j]-ah[j-d] ?

Yes, I believe there is an error too.
But I think it should be $f[j] \leftarrow f[j] - a\cdot h[j-(d'-d)]$, shouldn't it?
After all, the first time with $j=i=d'$, I think it should work out as $f[d'] \leftarrow f[d'] - a\cdot h[d'-(d'-d)]$. (Thinking)

Also, what do they mean at the part <<In line 5... unaltered.>> ? At line 5 of the algorithm, we have a<-u*f. Why is it said that the polynomial $f \cdot u \cdot h \cdot X^{i-d}$ is added to $h \cdot (q[0], \dots, q[d'-d])$ ? (Thinking)

This is the so called loop invariant.
In every iteration we have that $f_{original}=f+h\cdot q + r$.
Initially we have $q=r=0$, making it evidently true.
And at the end, when the algorithm is done, we have $f=0$ and $f_{original} = h\cdot q + r$, which is what we want to find. (Thinking)

 

[evinda]

Wouldn't we multiply $(f_{d'}\cdot u \cdot X^{d'-d})$ with $(h_dX^d+h_{d-1}X^{d-1} +... + h_0)$ to get $(f_{d'}X^{d'}+...)$? (Wondering)
So I think it is correct as it is given.

Ah, but I think that we subtract the polynomial $f \cdot u \cdot X^{i-d}$ from $(f[0], \dots, f[d'])$. Or am I wrong? (Thinking)

Yes, I believe there is an error too.
But I think it should be $f[j] \leftarrow f[j] - a\cdot h[j-(d'-d)]$, shouldn't it?
After all, the first time with $j=i=d'$, I think it should work out as $f[d'] \leftarrow f[d'] - a\cdot h[d'-(d'-d)]$. (Thinking)

Yes, I see... (Nod)

This is the so called loop invariant.
In every iteration we have that $f_{original}=f+h\cdot q + r$.
Initially we have $q=r=0$, making it evidently true.
And at the end, when the algorithm is done, we have $f=0$ and $f_{original} = h\cdot q + r$, which is what we want to find. (Thinking)

I haven't really understood this. How can we show that this equality holds after each iteration? (Thinking)

And why do we have at the end $f=0$ and $f_{original} = h\cdot q + r$? (Thinking)

 

[I like Serena]

Ah, but I think that we subtract the polynomial $f \cdot u \cdot X^{i-d}$ from $(f[0], \dots, f[d'])$. Or am I wrong?

Aren't we subtracting $a\cdot h[j-(d'-d)]$ from $f[j]$, where $a=u\cdot f$?
And repeat for every value of $j$ (Wondering)
So I think we're subtracting $f \cdot u \cdot X^{i-d} \cdot (h[0],\dots,h[d])$ from $(f[0], \dots, f[d'])$.
This is designed so that the coefficient of the highest power in $f$ becomes 0.
And simultaneously we add an entry to $q$ so that $f+h\cdot q$ remains the same.

I haven't really understood this. How can we show that this equality holds after each iteration? (Thinking)

And why do we have at the end $f=0$ and $f_{original} = h\cdot q + r$? (Thinking)

I didn't say it quite right, since $r$ only gets a value at the very end.
Initially we have $f_{original}=f+h\cdot q$, since $q=0$ at this time.
Then in each step we find another entry in $q$ (the quotient) and modify $f$ accordingly.
That is, we subtract a polynomial from $f$ such that the coefficient of its highest power becomes 0.
And finally, the remaining value of $f$, that now has a lower power than $h$, is assigned to $r$ (the remainder). (Thinking)

 

[evinda]

Aren't we subtracting $a\cdot h[j-(d'-d)]$ from $f[j]$, where $a=u\cdot f$?

I think that we should subtract $a\cdot h[j-(i-d)]$ from $f[j]$. Right? (Thinking)

And repeat for every value of $j$ (Wondering)
So I think we're subtracting $f \cdot u \cdot X^{i-d} \cdot (h[0],\dots,h[d])$ from $(f[0], \dots, f[d'])$.

How do we see that $u f h[d]$ corresponds to the polynomial $f u h X^{i-d}$ ? I am confused right now. (Worried)

This is designed so that the coefficient of the highest power in $f$ becomes 0.

I see...

I didn't say it quite right, since $r$ only gets a value at the very end.
Initially we have $f_{original}=f+h\cdot q$, since $q=0$ at this time.

Ok.

Then in each step we find another entry in $q$ (the quotient) and modify $f$ accordingly.

I was thinking how we can show that after each iteration the equality holds. For an arbitrary $i$, we get that $q[i-d] \leftarrow uf$, $f \leftarrow 0$ and $f[i-k] \leftarrow f[i-k]-ufh[j-(i-d)], k=1, \dots, d$.

Do we get the desired equality from these equalities? If so, how? (Thinking)

 

[evinda]

For $i=d'$, we get for example $q[0 \dots d'-d]=(0, \dots, u f[d'])$.
We set $a=u f[d']$ and we get

$$f[d']=0 \\ f[d'-1] \leftarrow f[d'-1]-a h[d-1] \\ \dots \\ f[d'-d] \leftarrow f[d'-d]-ah[0]$$

So after the first iteration we have that $f+hq=(0, f[d'-1]-a h[d-1], \dots, f[d'-d]-ah[0])+(h[0], \dots, h[d]) \cdot (0, \dots, u f[d])$. Right? If so, why is this equal to $f_{\text{original}}$ ? (Thinking)