Questions concerning Delayed Quantum Eraser

[jgm340]

After reading about the
http://en.wikipedia.org/wiki/Delayed_choice_quantum_eraser" experiment,
I thought of two interesting questions.

Here I have taken http://en.wikipedia.org/wiki/File:Kim_EtAl_Quantum_Eraser.svg" and simplified it:

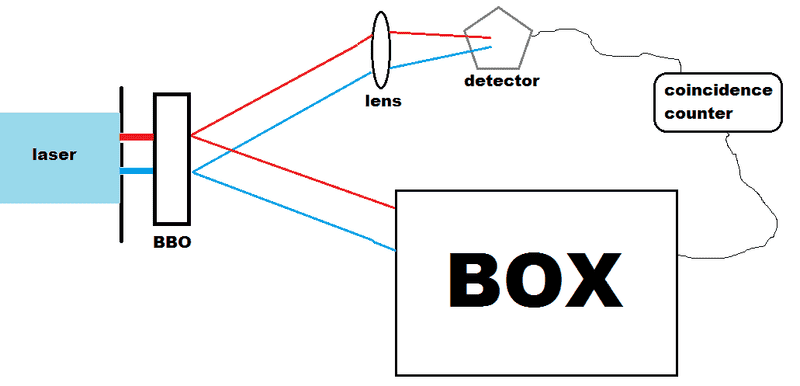
In the normal delayed choice quantum eraser experiment, the "BOX" will randomly do one of two things:

(i) gather information about which slit the photon has traveled through (either the red slit or the blue slit).

(ii) erase the information about which slit the photon has traveled through. It will erase the information one of two ways (call these methods of erasing "a" and "b"). It is detected which method of erasing was used.

There is a 50% chance of it doing (i) and a 50% chance of it doing (ii).

If we consider only photons detected to have passed through the red slit, we find no interference pattern. Likewise with those detected to have passed through the blue slit.

However, if we consider photons with path information erased by method "a", we DO see an interference pattern. Likewise with the path information erased by method "b".

The interesting thing is that the sum of these two interference patterns (formed through method "a" and method "b") is not an interference pattern!

Now here comes my first question:

Look at this diagram from the article:

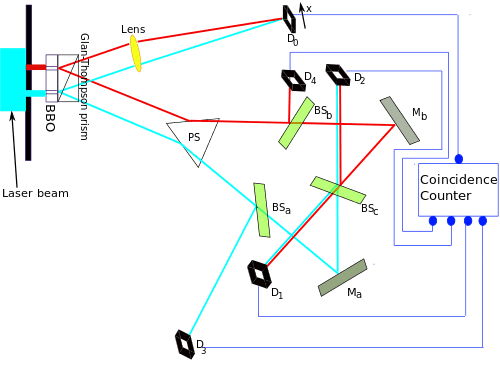
What would happen if were were to simply allow light reflecting off Ma (blue) to bypass BSc. Would the photons striking D2 still form an interference pattern (albeit different than before) on D1?

What would happen if, in addition to the change above, I replaced D1 with a series of mirrors that diverted the light towards D4 instead, syncing it up so that whatever path a "red" photon takes, it arrives at D4 in the same amount of time. Would the photons registered by D4 still not show an interference pattern? And would there still be an interference pattern for the photons registered by D2 (as above)?

If the answer to all the above is "yes", then it seems to me that if we consider all the photons registered by D2, D3, and D4 all together, then there would be an interference pattern on D0.

Now here's my second question:

Suppose the answer to the first question is yes. Then suppose I were to replace BSc by a mechanical switch, which has the ability to change very quickly from a beam-splitter to a mirror.

Now, suppose I hook up this mechanical switch to D0, so that whenever a photon is detected at D0, the switch changes BSc to a mirror after a time delay just perfect to allow the switch to happen before the entangled photon twin reaches BSc. Suppose also I have the switch turn back into a beam-splitter very quickly afterwards.

In this case, it ought to be that all the photons that were registered before by D2, D3, and D4 all together will still be registered. The only difference, I would think, would be which of D2, D3, or D4 detects the photon. If this is true, then the photons registered by D2, D3, and D4 altogether ought to show the same interference pattern on D0 as before. (The photons have already struck D0, so assuming causality isn't violated, the pattern ought to be the same.)

Now, here's where it starts not making sense: now that BSc is always switched to a mirror when the "red" photons strike it, the photons registered by D2 ought to give the same interference pattern as that of the photons registered by D1 and D2 combined in the original (unmodified) experiment. But this should show no interference!

Which line of reasoning is correct? One shows that the photons registered by D2, D3, and D4 all together ought to show an interference pattern on D0, and the other line of reasoning shows that it should not.

Have any experiments been done testing similar ideas to this?

 

[Joseph14]

I think you are missing a key part of this experiment. The beam splitter is asymmetric. It is a piece of glass with a coating on one side. Light from one direction reflects off the silver/glass interface introducing a $$\pi$$ phase shift. Light from the other direction reflects off a glass/silver interface with no phase shift. This difference is such that if red and blue are in phase the photon ends up at let's say D1 and out of phase by $$\pi$$ it will end up at D2. In essence all the box does is measures the phase difference. Once you can split the event into groups based on the phase measurements then you can look at the D0 events which correspond to these groups and see interference patterns.

In all cases where you removed or replaced the beam splitter you will not see interference because you will not have discovered the phase information.

 

[jgm340]

I think you are missing a key part of this experiment. The beam splitter is asymmetric. It is a piece of glass with a coating on one side. Light from one direction reflects off the silver/glass interface introducing a $$\pi$$ phase shift. Light from the other direction reflects off a glass/silver interface with no phase shift. This difference is such that if red and blue are in phase the photon ends up at let's say D1 and out of phase by $$\pi$$ it will end up at D2. In essence all the box does is measures the phase difference. Once you can split the event into groups based on the phase measurements then you can look at the D0 events which correspond to these groups and see interference patterns.

In all cases where you removed or replaced the beam splitter you will not see interference because you will not have discovered the phase information.

Wait a second, how can this be true?

After "PS", the "red" photons and "blue" photons are traveling on entirely different paths. Detectors D3 and D4 could only possibly detect photons that traveled through the "blue" and "red" slits, respectively.

I don't see where the phase information comes in, or why it would be necessary...

I had assumed that the purpose of the Glan-Thompson prism was to eliminate phase information.

 

[Joseph14]

As you move across the screen the path length difference will change making the 2 sources either in phase or out of phase, giving constructive and destructive interference. However, if the phase difference between the sources is random to start with then the phase difference at any point on the screen will be random as well (no interference). By measuring the phase difference you remove this random aspect. D3 and D4 do not measure phase difference therefore they show no interference. D1 and D2 do filter by phase difference so correspondingly they both show interference on the screen.

 

[Pio2001]

What would happen if were were to simply allow light reflecting off Ma (blue) to bypass BSc. Would the photons striking D2 still form an interference pattern (albeit different than before) on D1?

No

What would happen if, in addition to the change above, I replaced D1 with a series of mirrors that diverted the light towards D4 instead, syncing it up so that whatever path a "red" photon takes, it arrives at D4 in the same amount of time. Would the photons registered by D4 still not show an interference pattern?

No

And would there still be an interference pattern for the photons registered by D2 (as above)?

No

I had assumed that the purpose of the Glan-Thompson prism was to eliminate phase information.

According to wikipedia, the prism is there is order to "send it along divergent paths depending on whether it came from slit A or slit B".

I don't see where the phase information comes in, or why it would be necessary...

As Joseph14 said, phase difference is what is measured in this experiment. The interference pattern is a measurement of phase difference. Light parts means that the optical path are in phase, and dark parts means that the optical path are out of phase.

The same way, the BSc splitter measures the phase difference between the optical path that leads to its sides. If they are in phase, the photons will come out from one side, if they are out of phase, the photons will come out from the other side.

These two measurements are correlated.

 

[jgm340]

According to wikipedia, the prism is there is order to "send it along divergent paths depending on whether it came from slit A or slit B".

No, that text you are quoting is referring to the prism PS, not the Glan-Thompson prism. The Glan-Thompson prism somehow affects polarization, and I'm trying to figure out why it's necessary (it's not mentioned in the wikipedia description).

As Joseph14 said, phase difference is what is measured in this experiment. The interference pattern is a measurement of phase difference. Light parts means that the optical path are in phase, and dark parts means that the optical path are out of phase.

Yes, but the light is coherent to begin with! The interference pattern that forms overall should be based solely on the difference in path-length from slit A to detector D0 and from slit B to detector D0. If the difference is an integer multiple of the wavelength, then the photons from the same coherent light source (half going via slit A and the other half via slit B) will interfere constructively. For points on D0 where the path length difference from slit A versus slit B is half a wavelength more than an integer multiple of the wavelength, the photons will interfere destructively.

I've seen a variation of Young's double slit experiment performed (http://en.wikipedia.org/wiki/Double-slit_experiment), and there is an interference pattern without needing to track phase information.

If we simply let the photons go through slit A or B freely and don't try to find out which, then there will be an interference pattern that forms. Phase information is unnecessary because the light is coherent! In other words, if two photons hit the same point of detectors D0, then (as the speed of light is constant), they will be out of phase precisely by the longer distance one photon had to travel.

The same way, the BSc splitter measures the phase difference between the optical path that leads to its sides. If they are in phase, the photons will come out from one side, if they are out of phase, the photons will come out from the other side.

These two measurements are correlated.

They ought to be in phase solely by the coherence of the light! The distance is fixed, and the two paths are fixed. Moreover, this experiment is done only one photon at a time!

Could it be that BSc also acts differently depending on polarization? If so, that might explain the purpose of the Glan-Thompson prism, because in that case, the difference in polarization between the two paths would be different depending on the initial polarization of the photon...

From what I understand, the only way an interference pattern only disappears when you select for certain photons that have certain properties (eg. having gone through one slit or the other). The point of this experiment is showing that even when the selection of photons happens after they have hit D0, an interference pattern can still be erased. It's not so paradoxical if you think that the photon makes up it's mind about where on D0 to strike and which direction to go when it comes across a beam splitter before it even passes through the slits. Of course, then this raises the question about how FTL information travel. It makes intuitive sense to me how the statistics can work out how it does, but I'm trying to understand how physically this selection process is taking place.

 

[jgm340]

Ah, I read the paper, and the Glan-Thompson prism is actually just there to separate the entangled photons exiting the BBO. The BBO creates entagled photons with different polarizations (but not in different directions), and then the Glan-Thompson prism directs the two entangled photons in different directions based on their polarizations (as assigned by the BBO).

 

[zonde]

Yes, but the light is coherent to begin with! The interference pattern that forms overall should be based solely on the difference in path-length from slit A to detector D0 and from slit B to detector D0. If the difference is an integer multiple of the wavelength, then the photons from the same coherent light source (half going via slit A and the other half via slit B) will interfere constructively. For points on D0 where the path length difference from slit A versus slit B is half a wavelength more than an integer multiple of the wavelength, the photons will interfere destructively.

I've seen a variation of Young's double slit experiment performed (http://en.wikipedia.org/wiki/Double-slit_experiment), and there is an interference pattern without needing to track phase information.

Requirements for one photon interference and entangled photons interference are complimentary.
Maybe looking at this Cthugha's post might help:
https://www.physicsforums.com/showthread.php?p=2330857#post2330857"