thatboi
- 130
- 20
Hey all,
I am currently struggling with a change of variables step in my calculations.
Suppose the solutions ##f_{1}(x)## and ##f_{2}(x)## of the following system of differential equations is known:
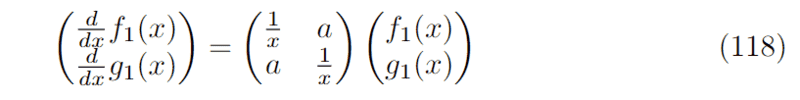
Now the system I wish to solve is:
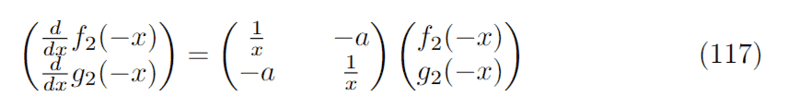
Upon first glance, it seems that the association ##f_{2}(-x) \leftrightarrow f_{1}(x)## and ##g_{2}(-x) \leftrightarrow g_{1}(x)## will do the trick and we would be done.
However, I tried making the change of variables ##y=-x## in equation (117) and got the following:
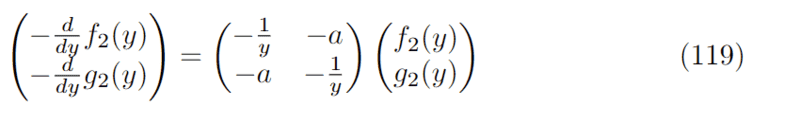
which is now the same form as equation (118).
Suddenly, it seems like the solution is now ##f_{2}(y) = f_{2}(-x) \leftrightarrow f_{1}(x)## and ##g_{2}(y) = g_{2}(-x) \leftrightarrow g_{1}(x)##
and I am left with a contradiction. Could someone point out to me where the mistake is? I feel like it is something simple that I am not seeing.
Thanks!
I am currently struggling with a change of variables step in my calculations.
Suppose the solutions ##f_{1}(x)## and ##f_{2}(x)## of the following system of differential equations is known:
Now the system I wish to solve is:
Upon first glance, it seems that the association ##f_{2}(-x) \leftrightarrow f_{1}(x)## and ##g_{2}(-x) \leftrightarrow g_{1}(x)## will do the trick and we would be done.
However, I tried making the change of variables ##y=-x## in equation (117) and got the following:
which is now the same form as equation (118).
Suddenly, it seems like the solution is now ##f_{2}(y) = f_{2}(-x) \leftrightarrow f_{1}(x)## and ##g_{2}(y) = g_{2}(-x) \leftrightarrow g_{1}(x)##
and I am left with a contradiction. Could someone point out to me where the mistake is? I feel like it is something simple that I am not seeing.
Thanks!