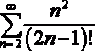motornoob101
- 45
- 0
For the factorial (2n+1)!, I thought the previous term is going to be (2(n-1)+1), which is equal to (2n-1).
Thus (2n+1)!= (2n+1)(2n-1)!
However, in the textbook, they have it as .
a_n= \frac{(2n-1)!}{(2n+1)!}=\frac{(2n-1)!}{(2n+1)(2n)(2n-1)!}
Are they wrong or I am wrong? Thanks!
Thus (2n+1)!= (2n+1)(2n-1)!
However, in the textbook, they have it as .
a_n= \frac{(2n-1)!}{(2n+1)!}=\frac{(2n-1)!}{(2n+1)(2n)(2n-1)!}
Are they wrong or I am wrong? Thanks!